Introduction

This paper is about the following type of problem: given independent (not necessarily identically distributed) random variables $X_1$, $X_2,\dots,$ $X_N$, find the `size' of ${\mathopen\vert S\mathclose\vert}$, where

$$S =\sum_{n=1}^N X_n .$$

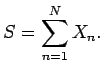
We will examine several ways to measure this size. The first will be through tail distributions, that is, $\Pr({\mathopen\vert S\mathclose\vert} > t)$. Finding an exact solution to this problem would be a dream of probabilists, so we have to temper our desires in some manner. In fact, this problem goes back to the foundations of probability in the following form: if the sequence $(X_n)$ consists of random variables that are mean zero, identically distributed and have finite variance, find the asymptotic value of $\Pr({\mathopen\vert S\mathclose\vert} > \sqrt N t)$ as $N \to \infty$. This is answered, of course, by the Central Limit Theorem, which tells us that the answer is the Gaussian distribution. There has been a tremendous amount of work on generalizing this. We refer the reader to almost any advanced work on probability.

Our approach is different. Instead of seeking asymptotic solutions, we will look for approximate solutions. That is, we seek a function $f(t)$, computed from $(X_n)$, such that there is a positive constant $c$ with

$$c^{-1} f(c t) \le \Pr(\vert S\vert>t) \le c \, f(c^{-1} t) .$$

The second measurement of the size of ${\mathopen\vert S\mathclose\vert}$ will be through the $p$th moments, ${\mathopen\Vert S\mathclose\Vert}_p = ({\mathbb{E}}{\left\vert S\right\vert}^p)^{1/p}$. Again, we shall be searching for approximate solutions, that is, finding a quantity $A$ such that there is a positive constant $c$ so that

$$c^{-1} A \le {\mathopen\Vert S\mathclose\Vert}_p \le c \, A .$$

While this may seem like quite a different problem, in fact, as we will show, there is a precise connection between the two, in that obtaining an approximate formula for ${\mathopen\Vert S\mathclose\Vert}_p$ with constants that are uniform as $p\to \infty$ is equivalent to obtaining an approximate formula for the tail distribution.

The third way that we shall look at is to find the size of ${\mathopen\vert S\mathclose\vert}$ in a rearrangement invariant space. This line of research was began by Carothers and Dilworth (1988) who obtained results for Lorentz spaces, and was completed by Johnson and Schechtman (1989). Our results will give a comparison of the size of ${\mathopen\vert S\mathclose\vert}$ in the rearrangement invariant space with ${\mathopen\Vert S\mathclose\Vert}_p$, obtaining a greater control on the sizes of the constants involved than the previous works.

Many of the results of this paper will be true for all sums of independent random variables, even those that are vector valued, with the following proviso. Instead of considering the sum $S = \sum_n X_n$, we will consider the maximal function $U = \sup_n {\left\vert\sum_{k=1}^n X_k\right\vert}$. We will define a property for sequences called the Lévy property, which will imply that $U$ is comparable to $S$. Sequences with this Lévy property will include positive random variables, symmetric random variables, and identically distributed random variables. The result of this paper that gives the tail distribution for $S$ is only valid for real valued sequences of random variables that satisfy the Lévy property. However the results connecting the $L_p$ and the rearrangement invariant norms to the tail distributions of $U$ are valid for all sequences of vector valued independent random variables. (Since this paper was submitted, Mark Rudelson pointed out to us that some of the inequalities can be extended from $U$ to $S$ by a simple symmetrization argument. We give details at the end of each relevant section.)

Let us first give the historical context for these results, considering first the problem of approximate formulae for the tail distribution. Perhaps the earliest works are the Paley-Zygmund inequality (see for example Kahane (1968, Theorem 3, Chapter 2)), and Kolmogorov's reverse maximal inequality (see for example Shiryaev (1980, Chapter 4, section 2.)) Both give (under an extra assumption) a lower bound on the probability that a sum of independent, mean zero random variables exceeds a fraction of its standard deviation and both may be regarded as a sort of converse to the Chebyshev's inequality. Next, in 1929, Kolmogorov, proved a two-sided exponential inequality for sums of independent, mean-zero, uniformly bounded, random variables (see for example Stout (1974, Theorem 5.2.2) or Ledoux and Talagrand (1991, Lemma 8.1)). All of these results require some restriction on the nature of the sequence $(X_n)$, and on the size of the level $t$.

Hahn and Klass (1997) obtained very good bounds on one sided tail probabilities for sums of independent, identically distributed, real valued random variables. Their result had no restrictions on the nature of the random variable, or on the size of the level $t$. In effect, their result worked by removing the very large parts of the random variables, and then using an exponential estimate on the rest. We will take a similar approach in this paper.

Let us next look at the $p$th moments. Khintchine (1923) gave an inequality for Rademacher (Bernoulli) sums. This very important formula has found extensive applications in analysis and probability. Khintchine's result was extended to any sequence of positive or mean zero random variables by the celebrated result of Rosenthal (1970). The order of the best constants as $p\to \infty$ was obtained by Johnson, Schechtman and Zinn (1983), and Pinelis (1994) refined this still further. Now even more precise results are known, and we refer the reader to Figiel, Hitczenko, Johnson, Schechtman and Zinn (1997) (see also Ibragimov and Sharakhmetov (1997)). However, the problem with all these results is that the constants were not uniformly bounded as $p\to \infty$.

Khintchine's inequality was generalized independently by Montgomery and Odlyzko (1988) and Montgomery-Smith (1990). They were able to give approximate bounds on the tail probability for Rademacher sums, with no restriction on the level $t$. Hitczenko (1993) obtained an approximate formula for the $L_p$ norm of Rademacher sums, where the constants were uniformly bounded as $p\to \infty$. (A more precise version of this last result was obtained in Hitczenko-Kwapien (1994) and it was used to give a simple proof of the lower bound in Kolmogorov's exponential inequality.)

Continuing in the direction of Montgomery and Odlyzko, Montgomery-Smith and Hitczenko, Gluskin and Kwapien (1995) extended tail and moment estimates from Rademacher sums to weighted sums of random variables with logarithmically concave tails (that is, $P({\left\vert X\right\vert}\ge t)=\exp(-\phi(t))$, where $\phi:[0,\infty)\to[0,\infty)$ is convex). After that, Hitczenko, Montgomery-Smith, and Oleszkiewicz (1997) treated the case of logarithmically convex tails (that is, the $\phi$ above is concave rather than convex). It should be emphasized that in the last paper, the result of Hahn and Klass (1997) played a critical role.

The breakthrough came with the paper of Lataa (1997), who solved the problem of finding upper and lower bounds for general sums of positive or symmetric random variables, with uniform constants as $p\to \infty$. His method made beautiful use of special properties of the function $t \mapsto t^p$. In a short note, Hitczenko and Montgomery-Smith (1999) showed how to use Lataa's result to derive upper and lower bounds on tail probabilities. Lataa's result is the primary motivation for this paper.

The main tool we will use is the Hoffmann-Jørgensen Inequality. In fact, we will use a stronger form of this inequality, due to Klass and Nowicki (1998). The principle in many of our proofs is the following idea. Given a sequence of random variables $(X_n)$, we choose an appropriate level $s>0$. Each random variable $X_n$ is split into the sum $X^{(\le s)}_n + X^{(>s)}_n$, where $X^{(\le s)}_n = X_n I_{{\left\vert X_n\right\vert}\le s}$, and $X^{(>s)}_n = X_n I_{{\left\vert X_n\right\vert} > s}$. It turns out that the quantity $(X_n^{(>s)})$ can either be disregarded, or it can be considered as a sequence of disjoint random variables. (By ``disjoint'' we mean that the random variables are disjointly supported as functions on the underlying probability space.) As for the quantity $\sum_n X_n^{(\le s)}$, it will turn out that the level $s$ allows one to apply the Hoffmann-Jørgensen/Klass-Nowicki Inequality so that it may be compared with quantities that we understand rather better.

Let us give an outline of this paper. In Section 2, we will give definitions. This will include the notion of decreasing rearrangement, that is, the inverse to the distribution function. Many results of this paper will be written in terms of the decreasing rearrangement. Section 3 is devoted to the Klass-Nowicki Inequality. Since our result is slightly stronger than that currently in the literature, we will include a full proof. In Section 4, we will introduce and discuss the Lévy property. This will include a ``reduced comparison principle'' for sequences with this property. Section 5 contains the formula for the tail distribution of sums of real valued random variables. Then in Section 6, we demonstrate the connection between $L_p$-norms of such sums and their tail distributions. In Section 7 we will discuss sums of independent random variables in rearrangement invariant spaces.