In this section, we will state and prove the formula for the tail distribution of the sum of independent, real valued, random variables that satisfy the Lévy Property.
If one restricts the formula to the case of sums of independent, identically distributed random variables, one obtains a formula very similar to the main result of Hahn and Klass (1997). The main differences are that their inequality involves one sided inequalities, and also that their inequality is more precise.
This formula also has a strong resemblance to the result of Lata![]() a.
As we shall show in Section 6, computing the
a.
As we shall show in Section 6, computing the ![]() norm of
norm of ![]() is
effectively equivalent to computing
is
effectively equivalent to computing
![]() . Then if one
notices that
. Then if one
notices that ![]() is very close to
is very close to ![]() for small positive
for small positive ![]() , one
can see that this result and the result of Lata
, one
can see that this result and the result of Lata![]() a are very closely related.
Presumably one could derive Lata
a are very closely related.
Presumably one could derive Lata![]() a's result by combining Theorem 5.1
with
Theorem 6.1. However the technical difficulties are quite tricky, and
since
Lata
a's result by combining Theorem 5.1
with
Theorem 6.1. However the technical difficulties are quite tricky, and
since
Lata![]() a's proof is elegant, we will not carry out this program here.
a's proof is elegant, we will not carry out this program here.
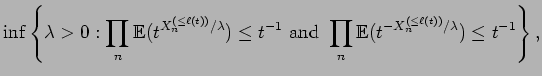 |
|||
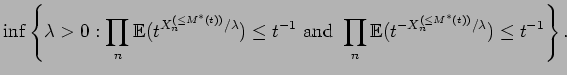 |
Let us start with gaining some understanding of
Orlicz spaces. There is a huge literature on Orlicz spaces,
see for example Lindenstrauss and Tzafriri (1977).
Suppose that
![]() is an increasing function (usually convex with
is an increasing function (usually convex with
![]() ). Then the Orlicz norm of a random variable
). Then the Orlicz norm of a random variable ![]() is defined
according to
the formula
is defined
according to
the formula
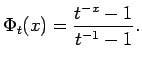
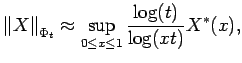
Proof: Suppose first that
![]() . Then
. Then
![]() , which implies that
, which implies that
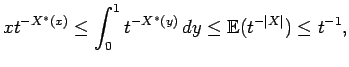
Conversely, suppose that
![]() for
for
![]() . Then
. Then
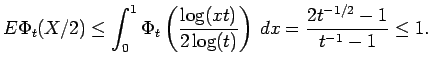
Proof of Theorem 5.1: Let us start with the proof that
![]() . Since the random variables
. Since the random variables
![]() are independent, we have that
are independent, we have that
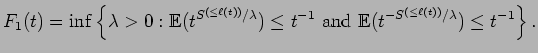
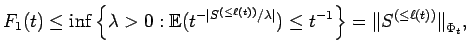
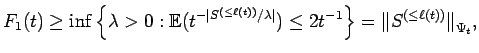
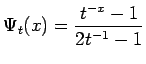 . However,
we quickly see that for
. However,
we quickly see that for Next, we apply Lemma 5.2, and we see that
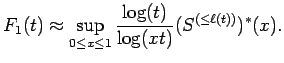
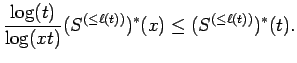
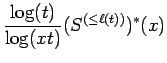 |
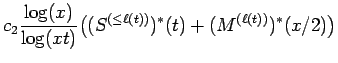 |
||
To show that
![]() is an almost identical
proof.
is an almost identical
proof.