The main result of this section establishes the
relationship between the ![]() norm of sums of random variables and
their tail distributions.
norm of sums of random variables and
their tail distributions.
We should note that we are not able to get universal control over
the constants as ![]() , as is shown by
simple examples once one understands that
, as is shown by
simple examples once one understands that
![]() converges to
the geometric mean of
converges to
the geometric mean of
![]() as
as ![]() .
.
Combining this with Corollary 3.2,
we immediately obtain the following result that compares
![]() to
to
![]() . This result extends results of Talagrand, (see
Ledoux and Talagrand (1991, Theorem 6.20), Kwapien and Woyczynski
(1992, Proposition 1.4.2 and comments following it; see also
Hitczenko (1994, Proposition 4.1)) and Johnson, Schechtman and Zinn
(1983). If this result is specialized to symmetric or positive real
valued random variables, then by considering the cases
. This result extends results of Talagrand, (see
Ledoux and Talagrand (1991, Theorem 6.20), Kwapien and Woyczynski
(1992, Proposition 1.4.2 and comments following it; see also
Hitczenko (1994, Proposition 4.1)) and Johnson, Schechtman and Zinn
(1983). If this result is specialized to symmetric or positive real
valued random variables, then by considering the cases ![]() or
or ![]() ,
it implies the inequality of Rosenthal
(1970), including the
result of Johnson, Schechtman and Zinn (1983) that gives
correct order of the constants as
,
it implies the inequality of Rosenthal
(1970), including the
result of Johnson, Schechtman and Zinn (1983) that gives
correct order of the constants as
![]() . Note that
. Note that
![]() by Proposition 2.1.
by Proposition 2.1.
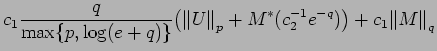 |
|||
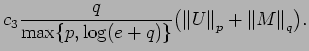 |
Let us proceed with the proofs. First we need a lemma that allows
us to deal with the ``large'' parts of ![]() , so that they might be
effectively considered as a sum of disjoint random variables.
, so that they might be
effectively considered as a sum of disjoint random variables.
Proof: In proving this result, we may suppose without loss of
generality that
![]() , that is, we may suppose that
, that is, we may suppose that
![]() .
.
If ![]() is a finite subset of
is a finite subset of
![]() , define the event
, define the event
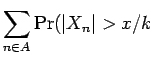 and and |
|||
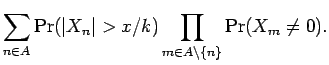 |
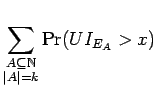 |
|||
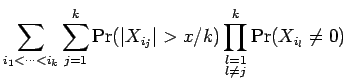 |
|||
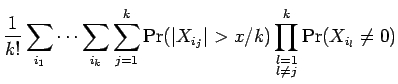 |
|||
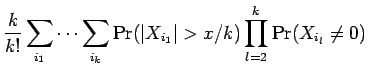 |
|||
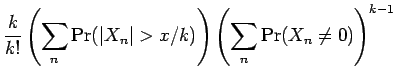 |
|||
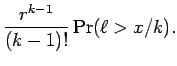 |
Proof: Apply Lemma 6.3 to obtain the ![]() .
Using the fact that
.
Using the fact that ![]() , we obtain that
, we obtain that
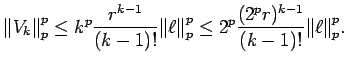
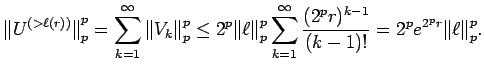
Proof of Theorem 6.1: Applying Proposition 2.1, we see that
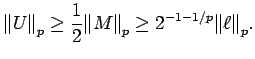
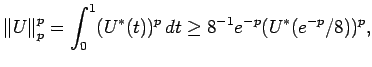
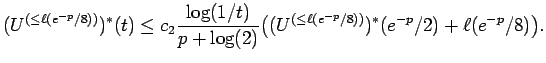
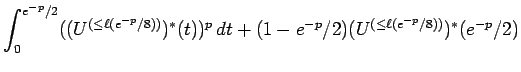 |
|||
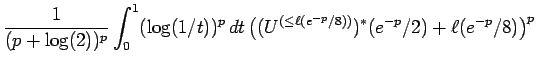 |
|||
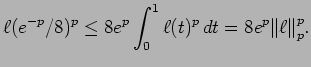
Finally we remark that from the results mentioned at the end of
Section 3 we can obtain one sided versions of
Theorem 6.1 with
![]() in place of
in place of ![]() , for
example, given
, for
example, given ![]() ,
,
Obviously if the sequence of random variables satisfy the Lévy property,
then we can obtain the two sided inequality, but otherwise the other
side of the inequality need not hold, as is shown by the example
![]() ,
, ![]() ,
, ![]() (
(![]() ).
).