Rearrangement invariant spaces are studied in much
of the
literature, see for example Lindenstrauss and Tzafriri (1977).
However, we will work with a definition that is a little
less restrictive.
A rearrangement invariant space on the
random variables is a quasi-normed Banach space ![]() of
random variables such that
of
random variables such that
![]() , and if
, and if
![]() and
and
![]() , then
, then
![]() and
and
![]() .
Obviously the spaces
.
Obviously the spaces ![]() for
for
![]() are rearrangement
invariant spaces.
are rearrangement
invariant spaces.
Given a rearrangement invariant space ![]() , we
define the quasi-constant of
, we
define the quasi-constant of ![]() to be the least constant
to be the least constant ![]() such
that
such
that
![]() for
all
for
all
![]() . Notice that
if
. Notice that
if
![]() , and
, and
![]() ,
then
,
then ![]() may be written as the sum of two disjoint
random variables
may be written as the sum of two disjoint
random variables ![]() and
and ![]() with
with
![]() ,
and hence
,
and hence
![]() .
.
Given two rearrangement invariant spaces ![]() and
and ![]() , we will say
that
, we will say
that ![]() embeds into
embeds into ![]() if there is a positive constant
if there is a positive constant ![]() such that if
such that if
![]() , then
, then
![]() and
and
![]() .
We will call the least such
.
We will call the least such ![]() the embedding constant of
the embedding constant of
![]() into
into ![]() .
.
Proof: Let us first obtain the left hand side
inequality. It follows by hypothesis that
![]() , where
, where ![]() is the embedding constant of
is the embedding constant of ![]() into
into
![]() . Furthermore,
. Furthermore,
![]() , and by Proposition 2.1,
, and by Proposition 2.1,
![]() . Hence
. Hence
![]() , where
, where ![]() is the quasi-constant of
is the quasi-constant of ![]() .
.
Now let us obtain the right hand inequality.
By Corollary 3.2, we
have that
there is a universal positive ![]() for
for
![]()
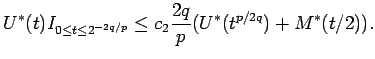
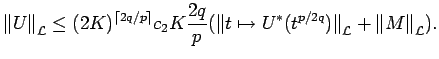
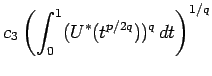 |
|||
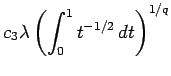 |
|||