The Klass-Nowicki Inequality

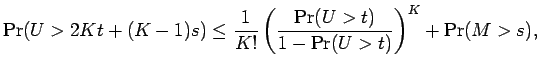
This section is devoted to the following result -- the Klass-Nowicki Inequality.

Theorem 3.1   Let $(X_n)$ be a sequence of Banach valued independent random variables. Then for all positive integers $K$ we have

$$\Pr(U > 2K t + (K-1)s) \le {\frac{1 }{ K!}} \left(\frac{\Pr(U > t) }{ 1 - \Pr(U > t) }\right)^{K}+ \Pr(M > s) ,$$

whenever $\Pr(U>t) < 1$.

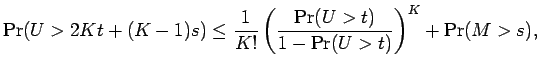
The original inequality of this form was for Rademacher (or Bernoulli) sums and $K=2$, and was due to Kahane (1968). This was extended by Hoffmann-Jørgensen (1974) to general sums, at least for positive or symmetric random variables, for the case $K=2$. Indeed, if one wants Theorem 3.1 for $K>2$, but without the $K!$ factor, this may be obtained by iterating the Hoffmann-Jørgensen Inequality, as was done by Johnson and Schechtman (1989, Lemmas 6 and 7). (Both Kahane and Hoffmann-Jørgensen obtained slightly different constants than those we have presented. Also, in neither case did a factor like $(1-\Pr(U>t))$ appear in their formulae.)

Klass and Nowicki (1998) were able to obtain Theorem 3.1, at least in the case when the random variables are positive or symmetric. (However their constants are better than ours.) Removing the positive or symmetric condition is really not so hard, but because it does not appear in the literature in this manner, we will give a complete proof of Theorem 3.1.

We also note that this inequality has some comparison with a result that appears in Ledoux and Talagrand (1991, Theorem 6.17.)

Proof: Let $N$ be the length of the sequence $(X_n)$. During this proof, let us write $(m,n]$ for the set of integers greater than $m$ and not greater than $n$.

We start with the observation

$$\Pr(U > 2K t+(K-1)s) \le \Pr(U >2K t+(K-1)s$$    and $$M \le s) + \Pr(M > s) .$$

Now, if we have that both $U > 2K t+(K-1)s$ and $M \le s$, then we ensure the existence of an increasing sequence of non-negative integers $m_0,\dots,$ $m_{K}$, bounded by $N$, and defined as follows. Set $m_0 = 0$. If we have picked $m_{l-1}$, let $m_l$ be the smallest positive integer greater than $m_{l-1}$ such that ${\mathopen\vert S_{(m_{l-1},m_l]}\mathclose\vert} > 2t$. For $l = 1$, it is clear that such an integer exists. Let us explain why the integer $m_l \le N$ exists if $2 \le l \le K$.

For $1 \le l' \le l-1$, and $m_{l'-1} < k \le m_{l'}-1$, we have that ${\mathopen\vert S_{(m_{l'-1},k]}\mathclose\vert} \le 2t$ and ${\mathopen\vert X_{m_{l'}}\mathclose\vert} \le s$. Hence for $1 \le l' \le l-1$

$${\mathopen\vert S_{m_{l'}}\mathclose\vert} = {\left\vert \sum_{j=1}^{l'} (S_{(m_{j-1},m_j-1]} + X_{m_j}) \right\vert} \le 2 l' t + l's,$$

and for $m_{l'-1} < k \le m_{l'}-1$

$${\mathopen\vert S_{k}\mathclose\vert} = {\left\vert \left(\sum_{... ...m_j-1]} + X_{m_j})\right) + S_{(m_{l'-1},k]} \right\vert} \le 2 l' t + (l'-1)s.$$

But we know that there exists a number $m$ such that ${\mathopen\vert S_m\mathclose\vert} > 2K t+(K-1)s$. Hence, we must have that $m > m_{l-1}$, and that ${\mathopen\vert S_{(m_{l-1},m]}\mathclose\vert} > 2K t + (K-1)s - 2(l-1)t - (l-1)s \ge 2t$.

Therefore

$$\Pr( U > 2K t+(K-1)s$$    and $$M \le s) \le \sum_{1 \le m_1 < \cdots < m_{K} \le N}p_{0,m_1} p_{m_1,m_2} \cdots p_{m_{K-1},m_K} ,$$

where

$$p_{m,n} = \Pr($$$|S_(m,k]| &le#le;2t$ for $m &le#le; k < n$, and $|S_(m,n]| > 2t$$$) .$$

Now let us show the following inequality:

$$\sum_{k=m+1}^n p_{m,k} \le {\frac{1}{ 1 - \Pr(U>t)}}\sum_{k=m+1}^n \tilde p_k ,$$

where

$$\tilde p_n = \Pr($$$|S_k| &le#le;t$ for $1 &le#le;k < n$, and $|S_n| > t$$$) .$$

Using independence, we have that

$$\sum_{k=m+1}^n p_{m,k} = \Pr(\sup_{m < k \le n} {\mathopen\vert S_k - S_m\mathclose\vert} > 2t)$$

$$= \Pr(\sup_{m < k \le n} {\mathopen\vert S_k - S_m\mathclose\vert} > 2t \big\vert U_m \le t)$$

$$\le \Pr(\sup_{m < k \le n} {\mathopen\vert S_k\mathclose\vert} > t \big\vert U_m \le t)$$

$$= {\frac{\Pr(\sup_{m<k\le n} {\mathopen\vert S_k\mathclose\vert} > ... ...{1 \le k \le m} {\mathopen\vert S_k\mathclose\vert} \le t) }{ \Pr(U_m \le t) }}$$

$$\le {\frac{1}{ 1 - \! \Pr(U>t)}}\sum_{k=m+1}^n \tilde p_k ,$$

as required.

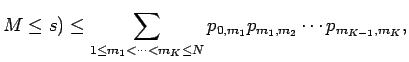
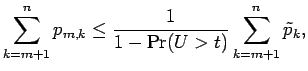
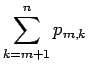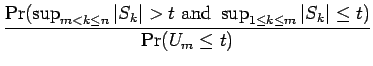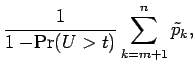Now we rearrange the sum as follows:

$$\sum_{1 \le m_1 < \cdots < m_{K} \le N}p_{0,m_1} p_{m_1,m_2} \cdots p_{m_{K-1},m_K}$$

$$= \sum_{1 \le m_1 < \cdots < m_{K-1} \le N}p_{0,m_1} p_{m_1,m_2} \cdots p_{m_{K-2},m_{K-1}} \sum_{m_K = m_{K-1}+1}^Np_{m_{K-1},m_K}$$

$$\le {\frac{1 }{ 1 - \Pr(U>t)}}\sum_{1 \le m_1 < \cdots < m_{K-1} \le ... ..._{m_1,m_2} \cdots p_{m_{K-2},m_{K-1}} \sum_{m_K = m_{K-1}+1}^N \tilde p_{m_K} .$$

Now we rearrange this last quantity to get

$$\sum_{1 \le m_1 < \cdots < m_{K} \le N}p_{0,m_1} p_{m_1,m_2} \cdots p_{m_{K-1},m_K}$$

$$\le {\frac{1 }{ 1 - \Pr(U>t)}} \sum_{1 \le m_1 < \cdots < m_{K-2} < m_K\le N} p_{0,m_1} p_{m_1,m_2} \cdots p_{m_{K-3},m_{K-2}} \tilde p_{m_K} \times$$

$$\times \sum_{m_{K-1} = m_{K-2}+1}^{m_K} p_{m_{K-2},m_{K-1}}$$

$$\le {\frac{1 }{ (1- \Pr(U>t))^2}} \sum_{1 \le m_1 < \cdots < m_{K-2} < m_K\le N} p_{0,m_1} p_{m_1,m_2} \cdots p_{m_{K-3},m_{K-2}} \tilde p_{m_K} \times$$

$$\times \sum_{m_{K-1} = m_{K-2}+1}^{m_K} \tilde p_{m_{K-1}} .$$

Repeating this argument $(K-2)$ more times, we eventually see that

$$\sum_{1 \le m_ < \cdots < m_K \le N} p_{0,m_1} p_{m_1,m_2} \cdots p_{m_{K-1},m_K}\cr$$

Now, since $K$ distinct numbers may be rearranged in $K!$ different ways, we have that

$$\sum_{1 \le m_1 < \cdots < m_K \le N} \tilde p_{m_1} \tilde p_{m_2} \cdots \tilde p_{m_K}$$

$$= {\frac{1 }{ K!}} \sum_{\substack{1 \le m_1,m_2,\dots,m_K \le N\\ ... ...dots,m_K \text{ distinct}}} \tilde p_{m_1} \tilde p_{m_2} \cdots \tilde p_{m_K}$$

$$\le {\frac{1 }{ K!}} \sum_{1 \le m_1,m_2,\dots,m_K \le N} \tilde p_{m_1} \tilde p_{m_2} \cdots \tilde p_{m_K}$$

$$= {\frac{1 }{ K!}} \left( \sum_{k=1}^N \tilde p_{k} \right)^K .$$

Since

$$\sum_{k=1}^N \tilde p_k= \Pr(U > t),$$

we obtain the result.

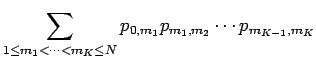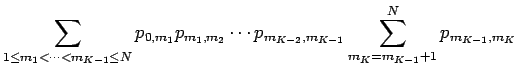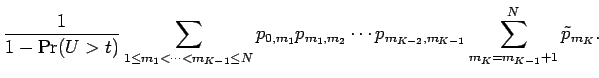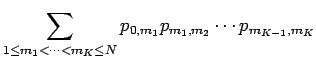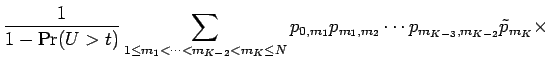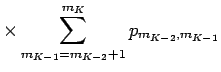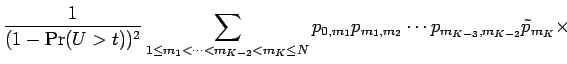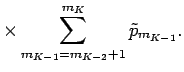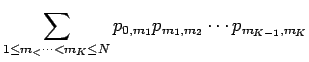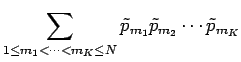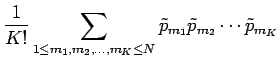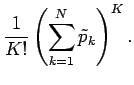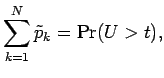
Let us now understand what this result means in terms of the decreasing rearrangement.

Corollary 3.2   There exists a universal positive constant $c_1$ such that for any sequence of Banach valued independent random variables $(X_n)$, and for $0<t\le s \le 1/2$ we have

$$U^*(t) \le c_1 {\frac{\log(1/t) }{ \max\{\log(1/s),\log\log(4/t)\}}} \bigl(U^*(s) + M^*(t/2)\bigr).$$

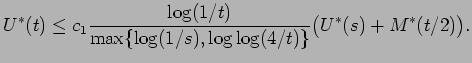
Proof: Notice that if $f,g:[0,\infty)\to[0,\infty]$ are non-increasing functions, then $(\max\{f,g\})^{-1} = \max\{f^{-1},g^{-1}\}$, and if $f \le g$, then $f^{-1} \le g^{-1}$, where here $f^{-1}$ denotes either the left or right continuous inverse of $f$. Since $A+B \le 2 \max\{A,B\}$ for any two positive numbers $A$ and $B$, from Theorem 3.1, and setting $s=t$, we have that if $\Pr(U>t) \le 1/2$, then for all positive integers $K$

$$\Pr(U > (3 K - 1) t)\le 2 \max \left\{{\frac{1 }{ K!}} \bigl(2\Pr(U > t)\bigr)^K, \Pr(M > t) \right\} .$$

Taking inverses, we see that if $(K!t/2)^{1/K} \le 1/2$, then

$${\frac{1 }{3K-1}} U^*(t) \le \max\left \{ U^*\left({\frac12}\left({\frac{K!t }{ 2}}\right)^{1/K}\right) , M^*\left({\frac{t}{2}} \right) \right\} .$$

Now, using the fact that $\max\{A,B\} \le A+B$ for any positive numbers $A$ and $B$, and by choosing $K$ to be the smallest integer such that $s \le(K!t / 2)^{1/K}$, and by some elementary but tedious algebra, the result follows.

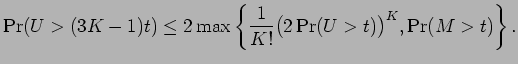
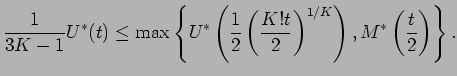
Since this paper was submitted, Mark Rudelson pointed out to us a couple of ways that Theorem 3.1 can be improved. First, we may obtain a result closer to that of Ledoux and Talagrand (1991, Theorem 6.17. Let $({\left\vert X_n\right\vert}^*)$ be the order statistics of $({\left\vert X_n\right\vert})$, that is, the values of $({\left\vert X_n\right\vert})$ rearranged in decreasing order. Then exactly the same proofs gives the following strengthening: for all positive integers $K$

$$\Pr(U > 2K t + (K-1)s) \le {\frac{1 }{ K!}} \left(\frac{\Pr(U > t... ...ht)^{K}+ \Pr\left(\sum_{n=1}^K {\left\vert X_n\right\vert}^* > (K-1)s\right) ,$$

whenever $\Pr(U>t) < 1$.

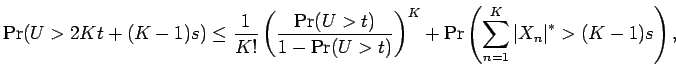
Secondly, a similar result is also true if we replace $U$ by ${\left\vert S\right\vert}$. This is certainly the case if the sequence $(X_n)$ consists of symmetric random variables, since they satisfy the Lévy property. Now let $(\bar X_n)$ be an independent copy of $(X_n)$, and let $\tilde X_n = X_n - \bar X_n$. Let $\bar S$ and $\tilde S$ respectively denote the sums formed from these two sequences of random variables. Thus we have the result for ${\left\vert\tilde S\right\vert}$, since it is a sum of symmetric random variables. But

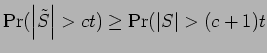$$\Pr({\left\vert\tilde S\right\vert} > c t) \ge \Pr({\left\vert S\right\vert} > (c+1)t$$    and $${\left\vert\bar S\right\vert}\le t) = \Pr({\left\vert S\right\vert} > (c+1)t) \Pr({\left\vert S\right\vert} \le t) .$$

Arguing in this way, we quickly see that there are constants $c_1$, $c_2$, and $c_3$ such that

$$\Pr(S > c_1 K(s+t)) \le \frac{\Pr(S > t)^K }{ K!(1 - c_2 \Pr(S > c_3 t))^{K+1} }+ \Pr(M > s) ,$$

whenever $\Pr(S > c_3 t) < c_2^{-1}$.

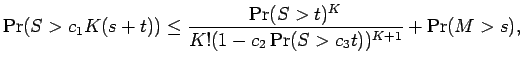
Thus a version of Corollary 3.2 is also true when $U$ is replaced by ${\left\vert S\right\vert}$.