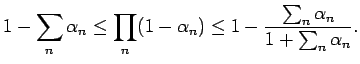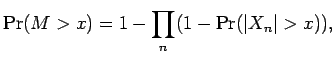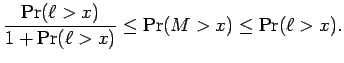Throughout this paper, a random variable will be a measurable function
from a probability space to some Banach space (often the real
line). The norm in the implicit Banach space will always be denoted by
![]() .
.
Suppose that
![]() is a non-increasing
function. Define the
left continuous inverse to be
is a non-increasing
function. Define the
left continuous inverse to be
In describing the tail distribution of a random variable ![]() , instead
of considering
the function
, instead
of considering
the function
![]() , we will
consider its right continuous inverse, which we will denote by
, we will
consider its right continuous inverse, which we will denote by ![]() .
In fact, this
quantity appears very much in the literature, and is more commonly
referred to as the decreasing rearrangement
(or more correctly the non-increasing rearrangement)
of
.
In fact, this
quantity appears very much in the literature, and is more commonly
referred to as the decreasing rearrangement
(or more correctly the non-increasing rearrangement)
of
![]() . Notice that if one considers
. Notice that if one considers ![]() to be a random variable on the
probability space
to be a random variable on the
probability space ![]() (with Lebesgue measure),
then
(with Lebesgue measure),
then ![]() has exactly the same law as
has exactly the same law as
![]() .
We might also consider the left continuous inverse
.
We might also consider the left continuous inverse
![]() . Notice that
. Notice that
![]() if and only if
if and only if
![]() .
.
If ![]() and
and ![]() are two quantities (that may depend upon certain
parameters), we will write
are two quantities (that may depend upon certain
parameters), we will write
![]() to mean that there exist
positive constants
to mean that there exist
positive constants ![]() and
and ![]() such that
such that
![]() . We will call
. We will call ![]() and
and ![]() the constants of approximation. If
the constants of approximation. If
![]() and
and ![]() are two (usually non-increasing) functions on
are two (usually non-increasing) functions on
![]() , we will write
, we will write
![]() if there exist
positive constants
if there exist
positive constants ![]() ,
, ![]() ,
, ![]() and
and ![]() such that
such that
![]() for all
for all ![]() . Again, we
will call
. Again, we
will call ![]() ,
, ![]() ,
, ![]() and
and ![]() the constants of
approximation.
the constants of
approximation.
Suppose that ![]() and
and ![]() are random variables. Then the statement
are random variables. Then the statement
![]() is the same as the
statement
is the same as the
statement
![]() . Since
. Since
![]() for
for ![]() the latter statement is equivalent to
the existence of positive constants
the latter statement is equivalent to
the existence of positive constants ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and
![]() such that
such that
![]() for
for
![]() .
.
To avoid bothersome convergence problems, we will always suppose that
our sequence of independent random variables ![]() is of finite
length. Given a sequence of independent random variables
is of finite
length. Given a sequence of independent random variables ![]() , when
no
confusion will arise, we will use the following notations. If
, when
no
confusion will arise, we will use the following notations. If ![]() is a
finite
subset of
is a
finite
subset of
![]() , we will let
, we will let
![]() , and
, and
![]() . If
. If ![]() is a positive integer, then
is a positive integer, then
![]() and
and
![]() . We will
define the maximal function
. We will
define the maximal function
![]() . Furthermore,
. Furthermore, ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() is the length of the sequence
is the length of the sequence ![]() .
.
If ![]() is a real number, we will write
is a real number, we will write
![]() and
and
![]() .
For
.
For
![]() , we will write
, we will write
![]() .
Similarly we define
.
Similarly we define
![]() ,
,
![]() , etc.
, etc.
Another quantity that we shall care about is the decreasing
rearrangement of the disjoint sum of random variables.
This notion was used by Johnson, Maurey,
Schechtman and Tzafriri (1979), Carothers and Dilworth (1988),
and Johnson and Schechtman (1989), all in the context of sums of
independent random variables.
The disjoint
sum of the sequence ![]() is the measurable function on the measure
space
is the measurable function on the measure
space
![]() that takes
that takes
![]() to
to
![]() . We shall denote the decreasing rearrangement of
the disjoint sum by
. We shall denote the decreasing rearrangement of
the disjoint sum by
![]() , that is,
, that is,
![]() is the least number such that
is the least number such that
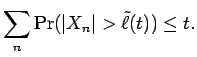
Proof: The first inequality follows easily
once one notices that both sides of this inequality are zero if ![]() .
.
To get the second inequality, note that, by an easy argument, if ![]() ,
,
![]() with
with
![]() , then
, then