


Next: Tail distributions
Up: Measuring the magnitude of
Previous: The Klass-Nowicki Inequality
The Lévy Property
Let 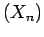 be a sequence of independent random variables. We will say
that
be a sequence of independent random variables. We will say
that 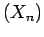 satisfies the Lévy property with constants
satisfies the Lévy property with constants 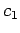 and
and 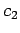 if whenever
if whenever
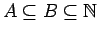 , with
, with 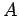 and
and 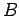 finite, then for
finite, then for 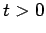
The casual reader should beware that this property has nothing to do
with Lévy processes.
The sequence 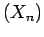 has the strong Lévy property with
constants
has the strong Lévy property with
constants
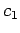 and
and 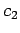 if for all
if for all 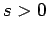 the sequence
the sequence
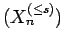 has
the Lévy property with constants
has
the Lévy property with constants 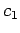 and
and 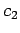 .
.
Here are examples of sequences with the strong Lévy property. (It
may be easily seen that in all these cases it is sufficient to
show that
they have the Lévy property.)
- Positive sequences,
with constants
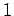 and
and 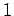 .
.
- Sequences of symmetric random variables
with constants
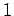 and
and
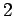 . This ``reflection property'' plays a major role in results
attributed to Lévy, hence the name of the property.
. This ``reflection property'' plays a major role in results
attributed to Lévy, hence the name of the property.
- Sequences of identically distributed random variables. This was shown
independently by Montgomery-Smith (1993) with constants
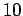 and
and 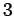 ,
and by Lata
,
and by Lata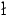 a (1993) with constants
a (1993) with constants 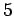 and
and 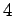 , or
, or 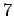 and
and
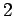 .
.
We see that sequences with the Lévy property
satisfy a maximal inequality.
Proof:
The first statement is an immediate corollary of the
following result known as Lévy-Ottaviani
inequality:
(Billingsley (1995, Theorem 22.5, p. 288) attributes
this result to Etemadi (1985) who proved it with constants 4 in both
places, but the same proof gives constants 3; see, for example,
Billingsley.
However the first named author learned this result from
Kwapien in 1980.)
The second statement follows from the first, since 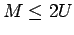 .
.
We end with a lemma that lists some elementary properties.
Part (i)
of the lemma might be thought of as a kind of reduced
comparison principle.
Lemma 4.2
Let 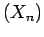 be a sequence of random variables
satisfying the strong Lévy property.
be a sequence of random variables
satisfying the strong Lévy property.
- There exist positive constants
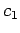 and
and 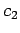 , depending
only upon the Lévy constants of
, depending
only upon the Lévy constants of 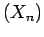 , such that if
, such that if 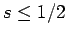 and
and
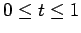 , then
, then
- There exist positive constants
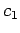 and
and 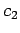 , depending only upon the
strong Lévy constants of
, depending only upon the
strong Lévy constants of 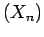 , such that if
, such that if
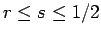 ,
and if
,
and if
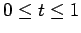 , then
, then
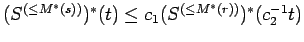 .
.
- If
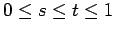 , then
, then
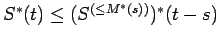 , and
, and
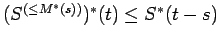 . In particular,
. In particular,
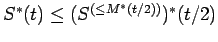 , and
, and
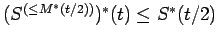 .
.
- For
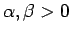 , we have
that
where the
constants of approximation depend only upon
, we have
that
where the
constants of approximation depend only upon 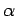 ,
, 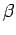 and the strong
Lévy constants of
and the strong
Lévy constants of 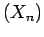 .
.
- We have that
where
the constants of approximation depend only upon the strong Lévy
constants of
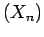 .
.
Proof:
Let us start with part (i).
For each set
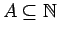 , define the event
, define the event
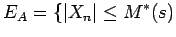
if and only if
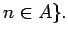
Note that the whole probability space is the disjoint union of these
events. Also
Furthermore, by independence, we see that
Hence
where in the first inequality we have used the fact that
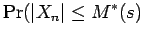
for
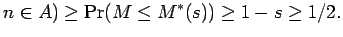
Part (ii) follows by applying
part (i) to
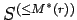 .
.
Part (iii) follows from the observation that
Hence, if
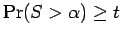 , then
, then
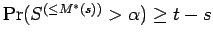 , and conversely, if
, and conversely, if
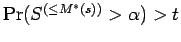 then
then
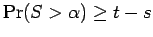 .
.
To show
part (iv),
we may suppose without loss of generality that 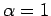 and
and 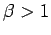 .
Clearly
.
Clearly
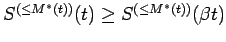 , so we need
only show an opposite inequality. From part (ii), there are
positive
constants
, so we need
only show an opposite inequality. From part (ii), there are
positive
constants 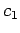 and
and 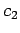 , depending only upon the strong Lévy constants of
, depending only upon the strong Lévy constants of
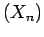 , such that for
, such that for
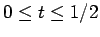
where
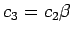 .
.
Part (v) follows easily by combining
part (iii), part (iv),
and Proposition 2.1.



Next: Tail distributions
Up: Measuring the magnitude of
Previous: The Klass-Nowicki Inequality
Stephen Montgomery-Smith
2002-10-30
![]() be a sequence of independent random variables. We will say
that
be a sequence of independent random variables. We will say
that ![]() satisfies the Lévy property with constants
satisfies the Lévy property with constants ![]() and
and ![]() if whenever
if whenever
![]() , with
, with ![]() and
and ![]() finite, then for
finite, then for ![]()
![]() has the strong Lévy property with
constants
has the strong Lévy property with
constants
![]() and
and ![]() if for all
if for all ![]() the sequence
the sequence
![]() has
the Lévy property with constants
has
the Lévy property with constants ![]() and
and ![]() .
.
![]() .
.
![]() , define the event
, define the event
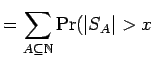 and
and 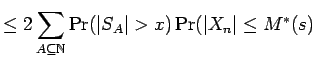 for
for ![]() and
and ![]() .
Clearly
.
Clearly
![]() , so we need
only show an opposite inequality. From part (ii), there are
positive
constants
, so we need
only show an opposite inequality. From part (ii), there are
positive
constants ![]() and
and ![]() , depending only upon the strong Lévy constants of
, depending only upon the strong Lévy constants of
![]() , such that for
, such that for
![]()