Bibliography

1

Billingsley, P. (1995) Probability and Measure, 3rd ed., Wiley & Sons, New York.

2

Carothers, N.L., Dilworth, S.J. (1988) Inequalities for sums of independent random variables, Proc. Amer. Math. Soc. 104, 221-226.

3

Etemadi, N. (1985) Tail probabilities for sums of independent Banach space valued random variables, Sankhya Ser. A 47, 209-214.

4

Figiel, T., Hitczenko, P., Johnson, W.B., Schechtman, G., Zinn, J. (1997) Extremal properties of Rademacher functions with applications to Khintchine and Rosenthal inequalities, Trans. Amer. Math. Soc., 349, 997-1027.

5

Giné, E.; Zinn, J. (1983) Central limit theorems and weak laws of large numbers in certain Banach spaces. Z. Wahrsch. Verw. Gebiete, 62, 323-354.

6

Gluskin, E.D., Kwapien, S. (1995) Tail and moment estimates for sums of independent random variables with logarithmically concave tails, Studia Math. 114, 303-309.

7

Hahn, M.G., Klass, M.J. (1997) Approximation of partial sums of arbitrary i.i.d. random variables and the precision of the usual exponential bound, Ann. Probab. 25, 1457-1470.

8

Hitczenko, P. (1993) Domination inequality for martingale transforms of a Rademacher sequence, Israel J. Math. 84, 161-178.

9

Hitczenko, P. (1994) On a domination of sums of random variables by sums of conditionally independent ones, Ann. Probab. 22, 453-468.

10

Hitczenko, P., Kwapien, S. (1994) On the Rademacher series, Probability in Banach Spaces, Nine, Sandbjerg, Denmark, J. Hoffmann-Jørgensen, J. Kuelbs, M.B. Marcus, Eds. Birkhäuser, Boston, 31-36.

11

Hitczenko, P., Montgomery-Smith, S.J. (1999) A note on sums of independent random variables, Advances in Stochastic Inequalities, Ed.: T. Hill and C. Houdré, Contemporary Mathematics 234, A.M.S., Providence R.I., 69-73.

12

Hitczenko, P., Montgomery-Smith, S.J., Oleszkiewicz, K. (1997) Moment inequalities for sums of certain independent symmetric random variables, Studia Math. 123, 15-42.

13

Hoffmann-Jørgensen, J. (1974) Sums of independent Banach space valued random variables. Studia Math. 52, 159-186.

14

Ibragimov, R., Sharakhmetov, Sh. (1997) On an exact constant for the Rosenthal inequality. Teor. Veroyatnost. i Primen. 42, 341 - 350 (translation in Theory Probab. Appl. 42 (1997), 294 - 302 (1998)).

15

Johnson, W.B., Maurey, B., Schechtman, G., Tzafriri, L. (1979) Symmetric structures in Banach spaces, Mem. Amer. Math. Soc. 217.

16

Johnson, W.B., Schechtman, G. (1989) Sums of independent random variables in rearrangement invariant function spaces, Ann. Probab. 17, 789-808.

17

Johnson, W.B., Schechtman, G., Zinn, J. (1983) Best constants in moment inequalities for linear combinations of independent and exchangeable random variables, Ann. Probab. 13, 234-253.

18

Kahane, J.-P. (1968) Some Random Series of Functions, 2nd ed., Cambridge University Press. Cambridge.

19

Khintchine, A., (1923) Über dyadische Brüche, Math. Z. 18, 109-116.

20

Klass, M. J., Nowicki, K (1998) An improvement of Hoffmann-Jørgensen's inequality, with applications, preprint.

21

Kwapien, S., Woyczynski, W.A. (1992) Random Series and Stochastic Integrals. Single and Multiple, Birkhäuser, Boston.

22

Lata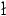a, R. (1993) A maximal inequality for sums of independent identically distributed random variables, Warsaw University Preprint .

23

Lata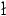a, R. (1997) Estimation of moments of sums of independent random variables, Ann. Probab., 25, 1502-1513.

24

Ledoux, M., Talagrand, M. (1991) Probability in Banach Spaces, Springer, Berlin, Heidelberg.

25

Lindenstrauss, J., Tzafriri, L. (1977) Classical Banach Spaces, II. Function Spaces, Springer, Berlin, Heidelberg.

26

Montgomery, H.L., Odlyzko, A.M. (1988) Large deviations of sums of independent random variables, Acta Arithmetica 49, 427-434.

27

Montgomery-Smith, S.J. (1990) The distribution of Rademacher sums. Proc. Amer. Math. Soc. 109, 517-522.

28

Montgomery-Smith, S.J. (1992) Comparison of Orlicz-Lorentz spaces. Studia Math. 103, 161-189.

29

Montgomery-Smith, S.J. (1993) Comparison of sums of independent identically distributed random variables, Probab. Math. Statist. 14, 281-285.

30

Pinelis, I. (1994), Optimum bounds for the distributions of martingales in Banach spaces, Ann. Probab. 22, 1679-1706.

31

Rosenthal, H.P. (1970) On the subspaces of 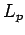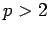$L_p$ ($p > 2$) spanned by sequences of independent symmetric random variables, Israel J. Math. 8, 273-303.

32

Shiryaev, A. N. (1980) Probability, Springer, Berlin, Heidelberg.

33

Stout, W.F. (1974) Almost Sure Convergence, Academic Press, New York.