Define measures
![]() and
and ![]() by their Fourier transforms:
by their Fourier transforms:
![]() ,
and
,
and
![]() .
Then we have the following decomposition theorem.
.
Then we have the following decomposition theorem.
| (32) | 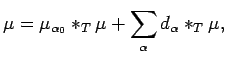 |
| (33) | 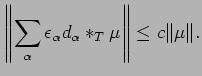 |
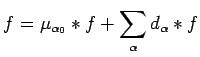
The next result, crucial to our proof of Theorem 5.1,
is already known in the case that
![]() with the lexicographic order
on the dual. This is due to Garling [15], and is a modification
of the celebrated inequalities of Burkholder.
Our result
can be obtained directly from the result in [15]
by combining the techniques of
[3] with the homomorphism theorem 4.5. However, we shall
take a different approach, in effect reproducing Garling's proof in this
more general setting.
with the lexicographic order
on the dual. This is due to Garling [15], and is a modification
of the celebrated inequalities of Burkholder.
Our result
can be obtained directly from the result in [15]
by combining the techniques of
[3] with the homomorphism theorem 4.5. However, we shall
take a different approach, in effect reproducing Garling's proof in this
more general setting.
Now let us show that if we have the result for compact ![]() , then
we have it for locally compact
, then
we have it for locally compact ![]() .
Let
.
Let
![]() denote the quotient homomorphism
of
denote the quotient homomorphism
of ![]() onto the discrete group
onto the discrete group
![]() (recall that
(recall that
![]() is open),
and define a measurable order on
is open),
and define a measurable order on
![]() to be
to be
![]() .
By Remarks 2.2 (c),
the decomposition of the group
.
By Remarks 2.2 (c),
the decomposition of the group
![]() that we get
by applying Theorem 2.1
to that group, is precisely the
image by
that we get
by applying Theorem 2.1
to that group, is precisely the
image by
![]() of the decomposition of the group
of the decomposition of the group ![]() .
Let
.
Let ![]() denote the
compact dual group of
denote the
compact dual group of
![]() . Thus if
Theorem 5.2 holds for
. Thus if
Theorem 5.2 holds for ![]() , then
applying Theorem 4.5, we see that
Theorem 5.2 holds for
, then
applying Theorem 4.5, we see that
Theorem 5.2 holds for ![]() .
.
Henceforth, let us suppose that ![]() is compact.
We will suppose that the Haar measure on
is compact.
We will suppose that the Haar measure on ![]() is normalized, so
that
is normalized, so
that ![]() with Haar measure is a probability space.
with Haar measure is a probability space.
Since each one of the subgroups ![]() , and
, and
![]() (
(
![]() ) is open, it follows that
their annihilators in
) is open, it follows that
their annihilators in ![]() ,
,
![]() , and
, and
![]() , are compact.
Let
, are compact.
Let
![]() and
and
![]() denote
the normalized Haar measures on
denote
the normalized Haar measures on
![]() and
and
![]() , respectively.
We have
, respectively.
We have
![]() (for all
(for all
![]() ),
and
),
and
![]() (for all
(for all
![]() ), so that
), so that
![]() .
.
For each ![]() ,
let
,
let
![]() denote the
denote the
![]() -algebra of subsets of
-algebra of subsets of ![]() of the form
of the form
![]() , where
, where ![]() is a Borel subset of
is a Borel subset of ![]() .
We have
.
We have
![]() , whenever
, whenever
![]() .
It is a simple matter to see that for
.
It is a simple matter to see that for
![]() , the conditional expectation of
, the conditional expectation of
![]() with respect to
with respect to
![]() is equal to
is equal to
![]() (see [11, Chapter 5, Section 2]).
(see [11, Chapter 5, Section 2]).
We may suppose without
loss of generality that
![]() .
Thus the
.
Thus the ![]() -algebras
-algebras
![]() form a filtration, and the
sequence
form a filtration, and the
sequence
![]() is a martingale
difference sequence with respect to this filtration.
is a martingale
difference sequence with respect to this filtration.
In that case, we have the following result
of Burkholder [7, Inequality (1.7)], and [8]. If
![]() , then there is a positive constant
, then there is a positive constant ![]() , depending only
upon
, depending only
upon ![]() , such that
, such that
Next, by convolving
with an approximate identity
for ![]() consisting of trigonometric
polynomials, we may assume
that
consisting of trigonometric
polynomials, we may assume
that ![]() is a
trigonometric polynomial.
Then we see that for each
is a
trigonometric polynomial.
Then we see that for each ![]() that
the function
that
the function
![]() ,
,
![]() , is
in
, is
in
![]() . To verify this, it is sufficient
to consider the case when
. To verify this, it is sufficient
to consider the case when
![]() is a character in
is a character in ![]() . Then
. Then
Now we have the following generalization of Jensen's Inequality,
due to Helson and Lowdenslager
[16, Theorem 2]. An independent proof based on the ideas of this
section is given in [3]. For all
![]()
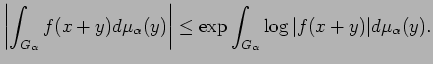
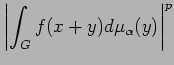 |
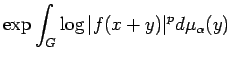 | ||
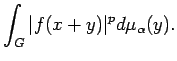 |
Let us continue with the proof of Theorem 5.2.
We may suppose that ![]() is a mean zero
trigonometric polynomial, and that
the spectrum of
is a mean zero
trigonometric polynomial, and that
the spectrum of ![]() is contained in
is contained in
![]() , that is to say
, that is to say
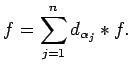
Proof of Theorem 5.1.
Transferring inequality (34) by using Theorem 1.8, we obtain that
for any set
![]() of indices
less than
of indices
less than ![]() , and
for any numbers
, and
for any numbers
![]() (
(
![]() ),
there is a positive constant
),
there is a positive constant ![]() , depending only upon the
representation
, depending only upon the
representation ![]() , such that
, such that
| (41) | 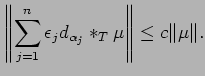 |
Now suppose that
![]() is a countable collection of
indices less than
is a countable collection of
indices less than ![]() .
Then by Bessaga and Pe
.
Then by Bessaga and Pe![]() czynski [5], the series
czynski [5], the series
![]() is unconditionally convergent.
In particular, for any
is unconditionally convergent.
In particular, for any ![]() , for only finitely many
, for only finitely many ![]() do we have
that
do we have
that
![]() . Since this is true for all
such countable sets, we deduce that the set of
. Since this is true for all
such countable sets, we deduce that the set of ![]() for which
for which
![]() is countable.
is countable.
Hence we have that
![]() is unconditionally convergent
to some measure, say
is unconditionally convergent
to some measure, say ![]() .
Clearly
.
Clearly ![]() is weakly measurable. To prove that
is weakly measurable. To prove that
![]() , it is enough by Proposition 1.4 to show that
for every
, it is enough by Proposition 1.4 to show that
for every
![]() , we have
, we have
![]() for almost all
for almost all ![]() .
.
We first note that since for every
![]() the series
the series
![]() converges to
converges to ![]() in
in ![]() , it follows that, for every
, it follows that, for every
![]() ,
the series
,
the series
![]() converges to
converges to ![]() in the weak-* topology of
in the weak-* topology of
![]() .
Now on the one hand, for
.
Now on the one hand, for ![]() and
and
![]() , we have
, we have
![]() ,
because of the (unconditional) convergence of
the series
,
because of the (unconditional) convergence of
the series
![]() to
to ![]() .
On the other hand, by considering the
.
On the other hand, by considering the
![]() function
function
![]() , we have that
, we have that
![]() ,
weak *. Thus
,
weak *. Thus
![]() for almost all
for almost all ![]() , and the
proof is complete.
, and the
proof is complete.