An order ![]() on
on ![]() is a subset
that satisfies the three axioms:
is a subset
that satisfies the three axioms:
![]() ;
;
![]() ; and
; and
![]() .
We recall from [1] the following property of orders.
.
We recall from [1] the following property of orders.
When ![]() is discrete, Theorem 2.1
can be deduced from
the proof of Hahn's Embedding Theorem for
orders (see [13, Theorem 16, p.59]).
The general case treated in Theorem 2.1
accounts for the measure theoretic aspect of orders.
The proof is
based on the study of orders of Hewitt and Koshi [18].
is discrete, Theorem 2.1
can be deduced from
the proof of Hahn's Embedding Theorem for
orders (see [13, Theorem 16, p.59]).
The general case treated in Theorem 2.1
accounts for the measure theoretic aspect of orders.
The proof is
based on the study of orders of Hewitt and Koshi [18].
For
![]() with
with
![]() , let
, let
If ![]() is
a subset of a topological space, we will use
is
a subset of a topological space, we will use
![]() and
and
![]() to denote the closure, respectively, the interior
of
to denote the closure, respectively, the interior
of ![]() .
.
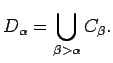
(c) Let
![]() be a continuous
homomorphism between two ordered groups. We say that
be a continuous
homomorphism between two ordered groups. We say that
![]() is order-preserving if
is order-preserving if
![]() .
Consequently, if
.
Consequently, if
![]() is continuous and order preserving, then
is continuous and order preserving, then
![]() .
.
For each
![]() , let
, let
![]() denote the
quotient homomorphism
denote the
quotient homomorphism
![]() .
Because
.
Because ![]() is a principal subgroup, we can define an order
on
is a principal subgroup, we can define an order
on
![]() by setting
by setting
![]() . Moreover, the principal convex subgroups
in
. Moreover, the principal convex subgroups
in
![]() are precisely the images by
are precisely the images by
![]() of the principal convex subgroups of
of the principal convex subgroups of
![]() containing
containing ![]() . (See [1, Section 2].)
. (See [1, Section 2].)
We end this section with a useful property of orders.
Proof. If ![]() is discrete, there is nothing to prove. If
is discrete, there is nothing to prove. If ![]() is not discrete, the subgroup
is not discrete, the subgroup
![]() is open and nonempty. Hence the set
is open and nonempty. Hence the set
![]() is nonempty, with 0 as a limit
point. Given an open nonempty neighborhood
is nonempty, with 0 as a limit
point. Given an open nonempty neighborhood ![]() of 0,
let
of 0,
let