Introduction

This paper is essentially providing a new approach to generalizations of the F.&M. Riesz Theorems, for example, such results as that of Helson and Lowdenslager [16,17]. They showed that if $G$ is a compact abelian group with ordered dual, and if $\mu$ is an analytic measure (that is, its Fourier transform is supported on the positive elements of the dual), then it follows that the singular and absolutely continuous parts (with respect to the Haar measure) are also analytic.

Another direction is that provided by Forelli [12] (itself a generalization of the result of de Leeuw and Glicksberg [9]), where one has an action of the real numbers $\Bbb R$ acting on a locally compact topological space $\Omega$, and a Baire measure $\mu$ on $\Omega$ that is analytic (in a sense that we make precise below) with respect to the action. Then again, the singular and absolutely continuous parts of $\mu$ (with respect to any so called quasi-invariant measure) are also analytic.

Indeed common generalizations of both these ideas have been provided, for example, by Yamaguchi [23], considering the action of any locally compact abelian group with ordered dual, on a locally compact topological space. For more generalizations we refer the reader to Hewitt, Koshi, and Takahashi [19].

In the paper [4], a new approach to proving these kinds of results was given, providing a transference principle for spaces of measures. In that paper, the action was from a locally compact abelian group into a space of isomorphisms on the space of measures of a sigma algebra. A primary requirement that the action had to satisfy was what was called sup path attaining, a property that was satisfied, for example, by the setting of Forelli (Baire measures on a locally compact topological space). Using this transference principle, the authors were able to give an extension and a new proof of Forelli's result. This was obtained by using a Littlewood-Paley decomposition of an analytic measure.

In this paper we wish to continue this process, applying this same transference principle to provide the common generalizations of the results of Forelli and Helson and Lowdenslager. What we provide in this paper is essentially a decomposition of an analytic measure as a sum of martingale differences with respect to a filtration defined by the order. For each martingale difference, the action of the group can be described precisely by a certain action of the group of real numbers, and so we can appeal to the results of [4].

In this way, we can reach the following generalization (see Theorem 6.4 below): if $\cal P$ is any bounded operator on the space of measures that commutes with the action (as does, for example, taking the singular part), and if $\mu$ is an analytic measure, then ${\cal P}\mu$ is also an analytic measure.

In the remainder of the introduction, we will establish our notation, including the notion of sup path attaining, and recall the transference principle from [4]. In Section 2, we will describe orders on locally compact abelian groups, including the extension of Hahn's Embedding Theorem provided in [1]. In Section 3, we define the notions of analyticity. This somewhat technical section continues into Section 4, which examines the role of homomorphism with respect to analyticity. The technical results basically provide proofs of what is believable, and so may be skipped on first reading. It will be seen that the concept of sup path attaining comes up again and again, and may be seen to be an integral part of all our proofs.

In Section 5, we are ready to present the decomposition of analytic measures. This depends heavily on transference of martingale inequalities of Burkholder and Garling, and then using the fact that weakly unconditionally summing series are unconditionally summing in norm for any series in a space of measures [5]. In Section 6, we then give applications of this decomposition, giving the generalizations that we alluded to above.

Throughout $G$ will denote a locally compact abelian group with dual group $\Gamma$. The symbols $\Bbb Z$, $\Bbb R$ and $\Bbb C$ denote the integers, the real and complex numbers, respectively. If $A$ is a set, we denote the indicator function of $A$ by $1_A$. For $1\leq p<\infty$, the space of Haar measurable functions $f$ on $G$ with $\int_G\vert f\vert^p dx<\infty$ will be denoted by $L^p(G)$. The space of essentially bounded functions on $G$ will be denoted by $L^\infty(G)$. The expressions ``locally null'' and ``locally almost everywhere'' will have the same meanings as in [20, Definition (11.26)].

Let ${\cal C}_0(G)$ denote the Banach space of continuous functions on $G$ vanishing at infinity. The space of all complex regular Borel measures on $G$, denoted by $M(G)$, consists of all complex measures arising from bounded linear functionals on ${\cal C}_0(G)$.

Let $(\Omega , \Sigma)$ denote a measurable space, where $\Omega$ is a set and $\Sigma$ is a sigma algebra of subsets of $\Omega$. Let $M(\Sigma)$ denote the Banach space of complex measures on $\Sigma$ with the total variation norm, and let ${\cal L}^\infty(\Sigma)$ denote the space of measurable bounded functions on $\Omega$.

Let $T:\ t\mapsto T_t$ denote a representation of $G$ by isomorphisms of $M(\Sigma)$. We suppose that $T$ is uniformly bounded, i.e., there is a positive constant $c$ such that for all $t\in G$, we have

$$\Vert T_t\Vert\leq c .$$ (1)

Definition 1.1   A measure $\mu\in M(\Sigma)$ is called weakly measurable (in symbols, $\mu\in{\cal M}_T(\Sigma)$) if for every $A\in \Sigma$ the mapping $t\mapsto T_t\mu(A)$ is Borel measurable on $G$.

Given a measure $\mu\in{\cal M}_T(\Sigma)$ and a Borel measure $\nu \in M(G)$, we define the `convolution' $\nu*_T\mu$ on $\Sigma$ by

$$\nu*_T\mu (A)=\int_G T_{-t}\mu(A) d\nu(t)$$ (2)

for all $A\in \Sigma$.

We will assume throughout this paper that the representation $T$ commutes with the convolution (2) in the following sense: for each $t\in G$,

$$T_t(\nu*_T\mu)=\nu*_T(T_t\mu).$$ (3)

Condition (3) holds if, for example, for all $t\in G$, the adjoint of $T_t$ maps ${\cal L}^\infty(\Sigma)$ into itself. In symbols,

$$T_t^*: {\cal L}^\infty(\Sigma) \rightarrow {\cal L}^\infty(\Sigma).$$ (4)

For proofs we refer the reader to [2]. Using (1) and (3), it can be shown that $\nu*_T\mu$ is a measure in ${\cal M}_T(\Sigma)$,

$$\Vert\nu*_T\mu\Vert\leq c\Vert\nu\Vert\Vert\mu\Vert,$$ (5)

where $c$ is as in (1), and

$$\sigma*_T(\nu*_T\mu)=(\sigma*\nu)*_T\mu,$$ (6)

for all $\sigma , \nu \in M(G)$ and $\mu\in{\cal M}_T(\Sigma)$ (see [2]).

Definition 1.2   A representation $T=(T_t)_{t\in G}$ of a locally compact abelian group $G$ in $M(\Sigma)$ is said to be sup path attaining if it is uniformly bounded, satisfies property (3), and if there is a constant $C$ such that for every weakly measurable $\mu\in{\cal M}_T(\Sigma)$ we have

$$\Vert \mu\Vert \leq C\sup \left\{ {\rm ess\ sup}_{t\in G} \left\v... ...t\vert :\ \ h\in {\cal L}^\infty(\Sigma),\ \Vert h\Vert _\infty\leq 1 \right\}.$$ (7)

The fact that the mapping $t\mapsto \int_\Omega h d (T_t\mu)$ is measurable is a simple consequence of the measurability of the mapping $t\mapsto T_t\mu(A)$ for every $A\in \Sigma$.

In [4] were provided many examples of sup path attaining representations. Rather than give this same list again, we give a couple of examples of particular interest.

Example 1.3   (a) (This is the setting of Forelli's Theorem.) Let $G$ be a locally compact abelian group, and $\Omega$ be a locally compact topological space. Suppose that $\left( T_t\right)_{t\in G}$ is a group of homeomorphisms of $\Omega$ onto itself such that the mapping

$$(t,\omega)\mapsto T_t\omega$$

is jointly continuous. Then the space of Baire measures on $\Omega$, that is, the minimal sigma algebra such that compactly supported continuous functions are measurable, is sup path attaining under the action $T_t\mu(A)=\mu(T_t(A))$, where $T_t(A)=\{T_t\omega:\ \omega\in A\}$. (Note that all Baire measures are weakly measurable.)

(b) Suppose that $G_1$ and $G_2$ are locally compact abelian groups and that $\phi:\ G_2\rightarrow G_1$ is a continuous homomorphism. Define an action of $G_2$ on $M(G_1)$ (the regular Borel measures on $G_1$) by translation by $\phi$. Hence, for $x\in G_2, \mu\in M(G_1)$, and any Borel subset $A\subset G_1$, let $T_x\mu(A)=\mu(A+\phi(x))$. Then every $\mu\in M(G_1)$ is weakly measurable, and the representation is sup path attaining with constants $c = 1$ and $C = 1$.

Proposition 1.4   Suppose that $T$ is sup path attaining and $\mu$ is weakly measurable such that for every $A\in \Sigma$ we have

$$T_t\mu(A)=0$$

for locally almost all $t\in G$. Then $\mu=0$.

The proof is immediate (see [2]).

We now recall some basic definitions from spectral theory.

If $I$ is an ideal in $L^1(G)$, let

$$Z(I)=\bigcap_{f\in I} \left\{ \chi\in\Gamma:\ \ \widehat{f}(\chi)=0 \right\}.$$

The set $Z(I)$ is called the zero set of $I$. For a weakly measurable $\mu\in M(\Sigma)$, let

$${\cal I}(\mu)=\{f\in L^1(G):\ \ f*_T\mu =0\}.$$

When we need to be specific about the representation, we will use the symbol ${\cal I}_T (\mu)$ instead of ${\cal I}(\mu)$.

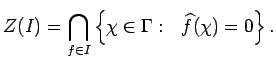
Using properties of the convolution $*_T$, it is straightforward to show that ${\cal I}(\mu)$ is a closed ideal in $L^1(G)$.

Definition 1.5   The $T$-spectrum of a weakly measurable $\mu\in{\cal M}_T(\Sigma)$ is defined by

$${\rm spec}_T (\mu)= \bigcap_{f\in {\cal I}(\mu)} \left\{ \chi\in\Gamma:\ \ \widehat{f}(\chi)=0 \right\}=Z({\cal I}(\mu)).$$ (8)

If $S\subset \Gamma$, let

$$L_S^1=L_S^1(G)=\left\{f\in L^1(G):\ \widehat{f}=0\ \mbox{outside of}\ S\right\}\,.$$

In order to state the main transference result, we introduce one more definition.

Definition 1.6   A subset $S\subset \Gamma$ is a ${\cal T}$-set if, given any compact $K\subset S$, each neighborhood of $0\in\Gamma$ contains a nonempty open set $W$ such that $W+K\subset S$.

Example 1.7   (a) If $\Gamma$ is a locally compact abelian group, then any open subset of $\Gamma$ is a ${\cal T}$-set. In particular, if $\Gamma$ is discrete then every subset of $\Gamma$ is a ${\cal T}$-set.
(b) The set $\left[ a,\infty\right. )$ is a ${\cal T}$-subset of $\Bbb R$, for all $a\in\Bbb R$.
(c) Let $a\in\Bbb R$ and $\psi:\ \Gamma \rightarrow \Bbb R$ be a continuous homomorphism. Then $S=\psi^{-1}([a,\infty))$ is a ${\cal T}$-set.
(d) Let $\Gamma=\Bbb R^2$ and $S=\{(x,y):\ y^2\leq x\}$. Then $S$ is a ${\cal T}$-subset of $\Bbb R^2$ such that there is no nonempty open set $W\subset \Bbb R^2$ such that $W+S\subset S$.

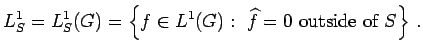
The main result of [4] is the following transference theorem.

Theorem 1.8   Let $T$ be a sup path attaining representation of a locally compact abelian group $G$ by isomorphisms of $M(\Sigma)$ and let $S$ be a ${\cal T}$-subset of $\Gamma$. Suppose that $\nu$ is a measure in $M(G)$ such that

$$\Vert\nu*f\Vert _1\leq \Vert f\Vert _1$$ (9)

for all $f$ in $L_S^1(G)$. Then for every weakly measurable $\mu\in M(\Sigma)$ with ${\rm spec}_T ( \mu )\subset S$ we have

$$\Vert\nu*_T\mu\Vert\leq c^3 C \Vert\mu\Vert,$$ (10)

where $c$ is as in (1) and $C$ is as in (7).