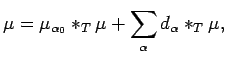Next: Bibliography
Up: Decomposition of analytic measures
Previous: Decomposition of Analytic Measures
Throughout this section,
we adopt the notation of Section 5, specifically,
the notation and assumptions of
Theorem 5.1.
Suppose that 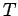 is a sup path attaining representation of
is a sup path attaining representation of  by isomorphisms of
by isomorphisms of  .
In [4], we proved the following
result concerning bounded operators
.
In [4], we proved the following
result concerning bounded operators 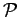 from
from 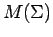 into
into 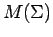 that commute with the representation
that commute with the representation 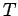 in the following sense:
in the following sense:
for all
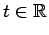 .
.
Theorem 6.1
Suppose that 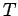 is a representation of
is a representation of 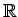 that is sup path
attaining,
and that
that is sup path
attaining,
and that 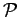 commutes with
commutes with 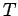 .
Let
.
Let
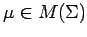 be weakly analytic.
Then
be weakly analytic.
Then
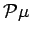 is also weakly analytic.
is also weakly analytic.
To describe an interesting application
of this theorem from [4], let us recall the following.
Definition 6.2
Let 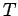 be a sup path attaining
representation of
be a sup path attaining
representation of 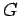 in
in 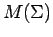 .
A weakly measurable
.
A weakly measurable 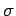 in
in 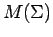 is
called quasi-invariant if
is
called quasi-invariant if
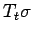 and
and 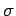 are mutually absolutely continuous for all
are mutually absolutely continuous for all 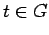 . Hence
if
. Hence
if 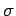 is quasi-invariant
and
is quasi-invariant
and
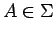 , then
, then
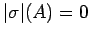 if and only if
if and only if
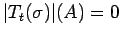 for all
for all 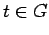 .
.
Using Theorem 6.1 we obtained in [4] the following extension of results of
de Leeuw-Glicksberg [9] and
Forelli [12], concerning quasi-invariant measures.
Theorem 6.3
Suppose that 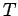 is a sup path attaining representation
of
is a sup path attaining representation
of 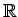 by isometries of
by isometries of 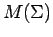 . Suppose
that
. Suppose
that
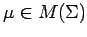 is weakly analytic, and
is weakly analytic, and
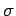 is quasi-invariant. Write
is quasi-invariant. Write
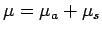 for the Lebesgue decomposition of
for the Lebesgue decomposition of 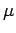 with respect to
with respect to 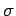 . Then both
. Then both
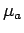 and
and 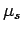 are weakly analytic. In particular,
the spectra of
are weakly analytic. In particular,
the spectra of 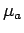 and
and 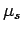 are
contained in
are
contained in
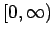 .
.
Our goal in this section is to extend Theorems 6.1
above to representations of a locally compact abelian group 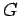 with ordered dual group
with ordered dual group 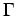 .
More specifically, we want to prove the following theorems.
.
More specifically, we want to prove the following theorems.
As shown in [4, Theorem (4.10)]
for the case 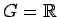 ,
an immediate corollary of Theorem 6.4
is the following result.
,
an immediate corollary of Theorem 6.4
is the following result.
Theorem 6.5
Suppose that 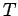 is a sup path attaining representation
of
is a sup path attaining representation
of 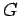 by isometries of
by isometries of 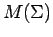 , such that
, such that
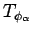 is sup path attaining for each
is sup path attaining for each 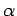 .
Suppose
that
.
Suppose
that
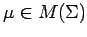 is weakly analytic with respect to
is weakly analytic with respect to 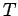 , and
, and
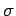 is quasi-invariant with respect to
is quasi-invariant with respect to 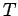 . Write
. Write
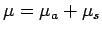 for the Lebesgue decomposition of
for the Lebesgue decomposition of 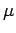 with respect to
with respect to 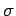 . Then both
. Then both
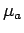 and
and 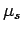 are weakly analytic with respect to
are weakly analytic with respect to 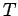 . In particular,
the
. In particular,
the 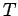 -spectra of
-spectra of 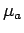 and
and 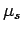 are
contained in
are
contained in
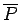 .
.
Proof of Theorem 6.4.
Write
as in (5.1), where the series converges unconditionally
in 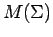 .
Then
.
Then
|
(42) |
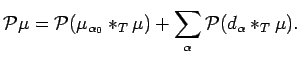 |
It is enough to show that the 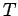 -spectrum of
each term is contained in
-spectrum of
each term is contained in
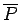 .
Consider the measure
.
Consider the measure
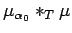 . We have
. We have
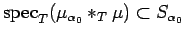 .
Hence by Theorem 4.4,
.
Hence by Theorem 4.4,
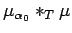 is
is
 -analytic. Applying Theorem 6.1, we see that
-analytic. Applying Theorem 6.1, we see that
|
(43) |
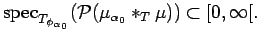 |
Since 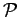 commutes with
commutes with 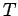 , it is easy to see
from Proposition 3.10 and Corollary 3.11 that
Hence by (43) and Theorem 4.4,
which shows the desired result for the first term
of the series in
(42). The other terms of the series
(42) are handled similarly.
, it is easy to see
from Proposition 3.10 and Corollary 3.11 that
Hence by (43) and Theorem 4.4,
which shows the desired result for the first term
of the series in
(42). The other terms of the series
(42) are handled similarly.
Acknowledgments The second author is
grateful for financial support from the National Science Foundation (U.S.A.) and the Research Board of the
University of Missouri.



Next: Bibliography
Up: Decomposition of analytic measures
Previous: Decomposition of Analytic Measures
Stephen Montgomery-Smith
2002-10-30
![]() is a sup path attaining representation of
is a sup path attaining representation of ![]() by isomorphisms of
by isomorphisms of ![]() .
In [4], we proved the following
result concerning bounded operators
.
In [4], we proved the following
result concerning bounded operators ![]() from
from ![]() into
into ![]() that commute with the representation
that commute with the representation ![]() in the following sense:
in the following sense:
![]() with ordered dual group
with ordered dual group ![]() .
More specifically, we want to prove the following theorems.
.
More specifically, we want to prove the following theorems.
![]() ,
an immediate corollary of Theorem 6.4
is the following result.
,
an immediate corollary of Theorem 6.4
is the following result.