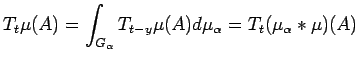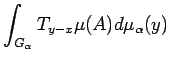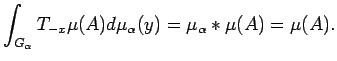Next: Homomorphism theorems
Up: Decomposition of analytic measures
Previous: Orders on locally compact
We continue with the notation of the previous section.
Using the order structure on 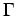 we define
some classes of analytic functions on
we define
some classes of analytic functions on 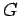 :
:
and
|
(16) |
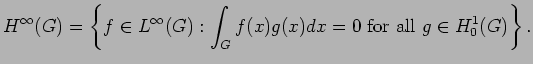 |
We clearly have
We can now give the definition of analytic measures in
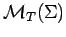 .
.
Definition 3.1
Let 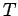 be a sup path attaining representation
of
be a sup path attaining representation
of 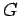 by isomorphisms of
by isomorphisms of 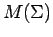 .
A measure
.
A measure
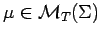 is
called weakly analytic if the mapping
is
called weakly analytic if the mapping
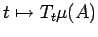 is in
is in
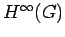 for every
for every
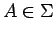 .
.
That the two definitions of analyticity are
equivalent will be shown later in this section.
Since
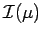 is translation-invariant,
it follows readily that
for all
is translation-invariant,
it follows readily that
for all 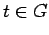 ,
,
and hence
|
(18) |
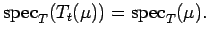 |
We now recall several
basic results from
spectral theory of bounded functions that will be needed in the sequel. Our reference is [21, Section 40].
If
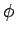 is in
is in
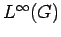 , write
, write
![$ \left[ \phi\right]$](img163.png) for the smallest weak-* closed translation-invariant subspace of
for the smallest weak-* closed translation-invariant subspace of
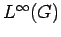 containing
containing 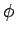 , and let
, and let
![$ {\cal I}([\phi])={\cal I}(\phi)$](img164.png) denote the closed translation-invariant ideal in
denote the closed translation-invariant ideal in 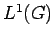 :
:
It is clear that
![$ {\cal I}(\phi)=\{f\in L^1(G): f*g=0, \forall g\in \left[\phi\right]\}$](img166.png) .
The spectrum of
.
The spectrum of 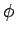 , denoted by
, denoted by
![$ \sigma \left[\phi\right]$](img167.png) ,
is the set of all continuous characters of
,
is the set of all continuous characters of 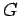 that belong to
that belong to
![$ \left[ \phi\right]$](img163.png) .
This closed subset of
.
This closed subset of 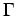 is also given by
is also given by
|
(19) |
![$\displaystyle \sigma \left[\phi\right]=Z({\cal I}(\phi)).$](img168.png) |
(See [21, Theorem (40.5)].)
Recall that a closed subset 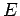 of
of 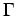 is
a set of spectral synthesis for
is
a set of spectral synthesis for 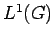 , or an
, or an 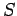 -set, if and only if
-set, if and only if
![$ {\cal I}([E])$](img170.png) is the only ideal in
is the only ideal in 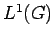 whose zero set
is
whose zero set
is 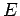 .
.
There are various equivalent definitions of 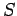 -sets.
Here is one that we will use at several occasions.
-sets.
Here is one that we will use at several occasions.
A set
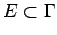 is an
is an 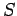 -set if and only if
every essentially bounded function
-set if and only if
every essentially bounded function 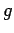 in
in
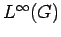 with
with
![$ \sigma[g]\subset E$](img173.png) is the weak-* limit
of linear combinations of characters from
is the weak-* limit
of linear combinations of characters from 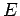 .
.
(See [21, (40.23) (a)].) This has
the following immediate consequence.
Proof. Part (i) is a simple consequence of
[21, Theorems (40.8) and (40.10)].
We give a proof for the sake of completeness.
Write 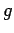 as the weak-* limit of
trigonometric polynomials,
as the weak-* limit of
trigonometric polynomials,
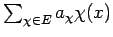 ,
with characters in
,
with characters in 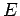 . Then
. Then
since
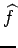 vanishes on
vanishes on 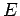 .
.
To prove (ii), assume that 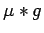 is not 0 a.e..
Then, there is
is not 0 a.e..
Then, there is 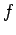 in
in 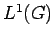 such that
such that
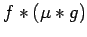 is not 0 a.e.. But this contradicts (i),
since
is not 0 a.e.. But this contradicts (i),
since
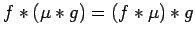 ,
, 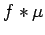 is in
is in 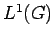 ,
and
,
and
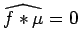 on
on 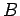 .
.
The following is a converse of sorts of Proposition
3.3 and follows easily from definitions.
Proof. Let 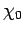 be any
element in
be any
element in
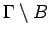 . We will show that
. We will show that
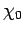 is not in the spectrum of
is not in the spectrum of 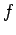 by constructing a
function
by constructing a
function 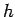 in
in 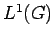 with
with
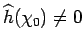 and
and 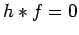 . Let
. Let 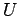 be an open neighborhood of
be an open neighborhood of
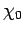 not intersecting
not intersecting 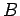 , and let
, and let 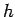 be in
be in 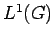 such that
such that
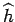 is equal to 1 at
is equal to 1 at 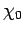 and to 0 outside
and to 0 outside 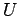 .
Direct computations show that the Fourier transform
of the function
.
Direct computations show that the Fourier transform
of the function
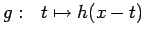 , when evaluated at
, when evaluated at
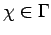 , gives
, gives
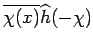 ,
and hence it vanishes on
,
and hence it vanishes on 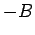 .
It follows from (20) that
.
It follows from (20) that 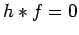 ,
which completes the proof.
,
which completes the proof.
A certain class of 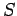 -sets, known as the
Calderón sets, or
-sets, known as the
Calderón sets, or 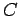 -sets,
is particularly useful to us.
These are defined as follows.
A subset
-sets,
is particularly useful to us.
These are defined as follows.
A subset 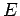 of
of 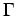 is
called a
is
called a 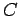 -set if every
-set if every 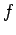 in
in
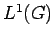 with Fourier transform
vanishing on
with Fourier transform
vanishing on 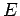 can be approximated
in the
can be approximated
in the 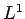 -norm by functions of the
form
-norm by functions of the
form 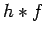 where
where
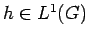 and
and
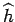 vanishes on
an open set containing
vanishes on
an open set containing 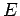 .
.
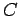 -sets enjoy the following properties
(see [21, (39.39)] or [22, Section 7.5]).
-sets enjoy the following properties
(see [21, (39.39)] or [22, Section 7.5]).
- Every
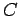 -set is an
-set is an 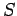 -set.
-set.
- Every closed subgroup of
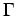 is a
is a 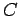 -set.
-set.
- The empty set is a
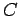 -set.
-set.
- If the boundary of a set
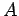 is a
is a 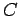 -set,
then
-set,
then 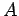 is a
is a 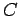 -set.
-set.
- Finite unions of
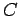 -sets are
-sets are 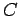 -sets.
-sets.
Since closed subgroups are 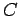 -sets, we conclude that
-sets, we conclude that
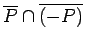 ,
and
,
and 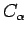 , for all
, for all 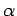 ,
are
,
are 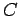 -sets.
>From the definition of
-sets.
>From the definition of
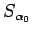 , (13),
and the fact that
, (13),
and the fact that
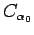 is open and closed, it
follows that the boundary of
is open and closed, it
follows that the boundary of
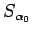 is the
closed subgroup
is the
closed subgroup
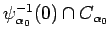 .
Hence
.
Hence
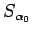 is a
is a 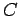 -set.
For
-set.
For
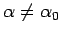 , the set
, the set
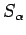 is open and closed,
and so it has
empty boundary, and thus it is a
is open and closed,
and so it has
empty boundary, and thus it is a 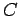 -set. Likewise
-set. Likewise
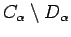 is a
is a 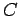 -set for all
-set for all
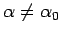 .
>From this we conclude that
arbitrary unions of
.
>From this we conclude that
arbitrary unions of 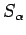 and
and
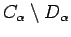 are
are 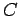 -sets, because an arbitrary union of
such sets, not including the index
-sets, because an arbitrary union of
such sets, not including the index 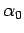 , is open and closed,
and so it is a
, is open and closed,
and so it is a 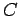 -set.
-set.
We summarize our findings as follows.
Proposition 3.5
Suppose that 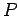 is a measurable order on
is a measurable order on 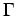 .
We have:
.
We have:
(i)
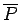 and
and
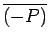 are
are 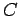 -sets;
-sets;
(ii) 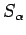 is a
is a 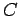 -set for all
-set for all 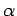 ;
;
(iii) arbitrary unions of 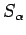 and
and
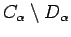 are
are 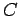 -sets.
-sets.
As an immediate application, we
have the following characterizations.
Corollary 3.6
Suppose that 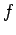 is in
is in
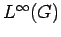 ,
then
,
then
(i)
![$ \sigma[f] \subset S_\alpha$](img215.png) if and only if
if and only if
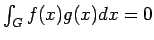 for all
for all
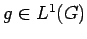 such that
such that
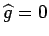 on
on 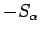 ;
;
(ii)
![$ \sigma[f] \subset \Gamma\setminus C_\alpha$](img219.png) if and only if
if and only if
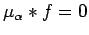 ;
;
(iii)
![$ \sigma[f] \subset \overline{P}$](img221.png) if and only if
if and only if
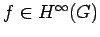 .
.
Proof. Assertions (i) and (iii) are clear from
Propositions 3.5 and 3.4.
To prove
(ii), use Fubini's Theorem to first establish
that for any
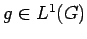 , and any
, and any
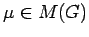 , we have
, we have
Now suppose that
![$ \sigma[f] \subset \Gamma\setminus C_\alpha$](img219.png) , and let
, and let 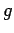 be any function in
be any function in
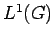 . From Propositions 3.5 and
3.4, we have that
. From Propositions 3.5 and
3.4, we have that
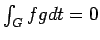 for all
for all 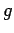 with Fourier transform vanishing on
with Fourier transform vanishing on
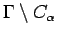 , equivalently, for all
, equivalently, for all
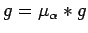 .
Hence,
.
Hence,
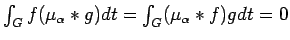 for all
for all 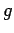 in
in 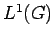 , from which it follows that
, from which it follows that
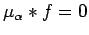 .
The converse is proved similarly, and we omit the details.
.
The converse is proved similarly, and we omit the details.
Aiming for a characterization of weakly analytic measures in terms of their spectra, we present one more result.
Proposition 3.7
Let 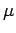 be weakly measurable in
be weakly measurable in 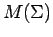 .
.
(i) Suppose that 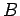 is a nonvoid closed
subset of
is a nonvoid closed
subset of 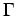 and
and
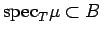 .
Then
.
Then
![$ \sigma[t\mapsto T_t\mu(A)]\subset B$](img230.png) for all
for all
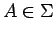 .
.
(ii) Conversely, suppose that 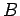 is an
is an 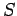 -set in
-set in 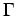 and that
and that
![$ \sigma[t\mapsto T_t\mu(A)]\subset B$](img230.png) for all
for all
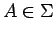 , then
, then
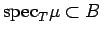 .
.
Proof. We clearly have
![$ {\cal I}(\mu)\subset {\cal I}([t\mapsto T_t\mu(A)])$](img231.png) .
Hence,
.
Hence,
![$ {\rm spec}_T \mu=Z({\cal I}(\mu))\supset
Z({\cal I}([t\mapsto T_t\mu(A)]))=\sigma[t\mapsto T_t\mu(A)],$](img232.png) and (i) follows.
and (i) follows.
Now suppose that 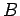 is an
is an 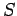 -set and let
-set and let
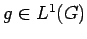 be such that
be such that
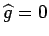 on
on 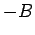 . Then, for all
. Then, for all
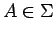 ,
we have from Proposition 3.4:
Equivalently, we
have that
Since the Fourier transform of the function
,
we have from Proposition 3.4:
Equivalently, we
have that
Since the Fourier transform of the function
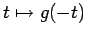 vanishes on
vanishes on 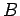 ,
we see that
,
we see that
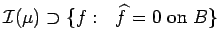 .
Thus
.
Thus
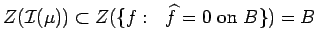 ,
which completes the proof.
,
which completes the proof.
Straightforward applications of Propositions
3.5
and 3.7 yield the
desired characterization of weakly analytic measures.
Corollary 3.8
Suppose that
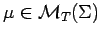 . Then,
. Then,
(i) 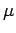 is weakly
is weakly 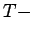 analytic if and only if
analytic if and only if
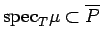 if and only if
if and only if
![$ \sigma [t\mapsto T_t\mu (A)]\subset \overline{P}$](img240.png) , for every
, for every
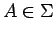 ;
;
(ii)
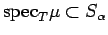 if and only if
if and only if
![$ \sigma[t\mapsto T_t\mu(A)]\subset S_\alpha$](img242.png) for every
for every
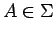 .
.
(iii)
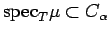 if and only if
if and only if
![$ \sigma[t\mapsto T_t\mu(A)]\subset C_\alpha$](img244.png) for every
for every
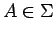 .
.
(iv)
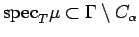 if and only if
if and only if
![$ \sigma[t\mapsto T_t\mu(A)]\subset \Gamma\setminus C_\alpha$](img246.png) for every
for every
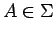 .
.
The remaining results of this section are
simple properties of measures in
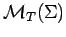 that will be needed later.
Although the statements are
direct analogues of classical facts about measures on groups, these
generalization require in some places the sup path
attaining property of
that will be needed later.
Although the statements are
direct analogues of classical facts about measures on groups, these
generalization require in some places the sup path
attaining property of 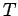 .
.
Proposition 3.9
Suppose that
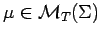 and
and
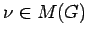 .
Then
.
Then
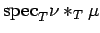 is contained in the support
of
is contained in the support
of
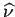 , and
, and
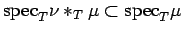 .
.
Proof.
Given 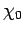 not in the support of
not in the support of
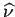 , to
conclude that it is also not in the spectrum of
, to
conclude that it is also not in the spectrum of
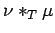 it is enough to find a function
it is enough to find a function 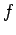 in
in 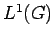 with
with
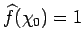 and
and
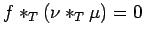 . Simply choose
. Simply choose 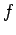 with Fourier transform
vanishing on the support of
with Fourier transform
vanishing on the support of
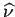 and taking value 1
at
and taking value 1
at 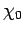 . By Fourier inversion, we have
. By Fourier inversion, we have
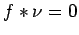 , and since
, and since
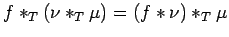 , the
first part of the proposition follows.
For the second part,
we have
, the
first part of the proposition follows.
For the second part,
we have
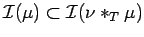 ,
which implies the desired inclusion.
,
which implies the desired inclusion.
We next prove a property of
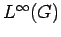 functions
similar to the characterization of
functions
similar to the characterization of 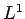 functions which are
constant on cosets of a subgroup [21, Theorem (28.55)].
functions which are
constant on cosets of a subgroup [21, Theorem (28.55)].
Proposition 3.10
Suppose that 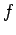 is in
is in
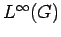 and that
and that 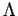 is
an open subgroup of
is
an open subgroup of 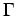 . Let
. Let 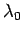 denote
the normalized Haar measure on the compact group
denote
the normalized Haar measure on the compact group
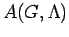 , the annihilator in
, the annihilator in 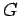 of
of
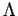 (see [20, (23.23)]. Then,
(see [20, (23.23)]. Then,
![$ \sigma[f]\subset \Lambda$](img258.png) if and only if
if and only if
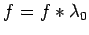 a. e. This is also
the case if and only if
a. e. This is also
the case if and only if 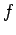 is constant on
cosets of
is constant on
cosets of
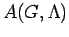 .
.
Proof. Suppose that the spectrum of 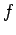 is contained
in
is contained
in 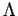 . Since
. Since 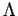 is an
is an 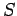 -set, it follows that
-set, it follows that 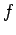 is the weak-* limit of trigonometric polynomials with
spectra contained in
is the weak-* limit of trigonometric polynomials with
spectra contained in 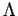 . Let
. Let
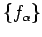 be a net
of such trigonometric polynomials converging
to
be a net
of such trigonometric polynomials converging
to 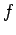 weak-*. Note that, for any
weak-*. Note that, for any 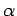 ,
we have
,
we have
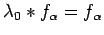 . For
. For 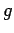 in
in 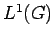 , we have
In particular, we have
and so
Since this holds for any
, we have
In particular, we have
and so
Since this holds for any 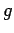 in
in 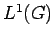 , we conclude that
, we conclude that
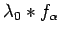 converges weak-* to
converges weak-* to
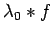 .
But
.
But
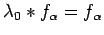 , and
, and 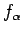 converges weak-* to
converges weak-* to 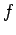 , hence
, hence
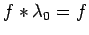 . The remaining assertions of the
lemma are easy to prove. We omit the details.
. The remaining assertions of the
lemma are easy to prove. We omit the details.
In what follows, we use the symbol
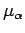 to denote the
normalized Haar measure on the compact subgroup
to denote the
normalized Haar measure on the compact subgroup
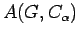 , the annihilator in
, the annihilator in 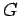 of
of 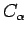 .
This measure is also characterized by its Fourier
transform:
.
This measure is also characterized by its Fourier
transform:
(see [20, (23.19)]).
Corollary 3.11
Suppose that
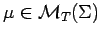 . Then,
. Then,
(i)
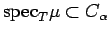 if and only if
if and only if
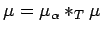 ;
;
(ii)
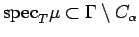 if and only if
if and only if
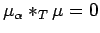 .
.
Proof. (i) If
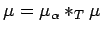 ,
then, by Proposition 3.10,
,
then, by Proposition 3.10,
![$ \sigma[t\mapsto \mu_\alpha*_T T_t\mu(A)]\subset C_\alpha$](img274.png) .
Hence by Corollary 3.8,
.
Hence by Corollary 3.8,
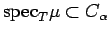 .
For the other direction, suppose that
.
For the other direction, suppose that
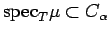 . Then by Corollary 3.8
we have that the spectrum of the function
. Then by Corollary 3.8
we have that the spectrum of the function
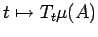 is contained in
is contained in 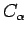 for every
for every
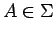 . By Proposition 3.10,
we have that
for almost all
. By Proposition 3.10,
we have that
for almost all 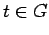 . Since this holds for all
. Since this holds for all
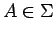 ,
the desired conclusion
follows from Proposition 1.4.
,
the desired conclusion
follows from Proposition 1.4.
Part (ii) follows from Corollary 3.6 (ii), Proposition
3.7(ii), and the fact that
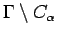 is an
is an 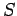 -set.
-set.
Corollary 3.12
Suppose that
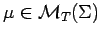 and
and
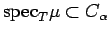 ,
and let
,
and let
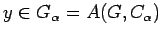 . Then
. Then
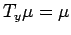 .
.
Proof. For any
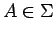 , we have from Corollary
3.11
, we have from Corollary
3.11



Next: Homomorphism theorems
Up: Decomposition of analytic measures
Previous: Orders on locally compact
Stephen Montgomery-Smith
2002-10-30
![]() we define
some classes of analytic functions on
we define
some classes of analytic functions on ![]() :
:
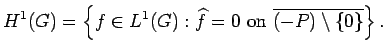
![]() is translation-invariant,
it follows readily that
for all
is translation-invariant,
it follows readily that
for all ![]() ,
,
![]() is in
is in
![]() , write
, write
![]() for the smallest weak-* closed translation-invariant subspace of
for the smallest weak-* closed translation-invariant subspace of
![]() containing
containing ![]() , and let
, and let
![]() denote the closed translation-invariant ideal in
denote the closed translation-invariant ideal in ![]() :
:
![]() of
of ![]() is
a set of spectral synthesis for
is
a set of spectral synthesis for ![]() , or an
, or an ![]() -set, if and only if
-set, if and only if
![]() is the only ideal in
is the only ideal in ![]() whose zero set
is
whose zero set
is ![]() .
.
![]() -sets.
Here is one that we will use at several occasions.
-sets.
Here is one that we will use at several occasions.
![]() is an
is an ![]() -set if and only if
every essentially bounded function
-set if and only if
every essentially bounded function ![]() in
in
![]() with
with
![]() is the weak-* limit
of linear combinations of characters from
is the weak-* limit
of linear combinations of characters from ![]() .
.
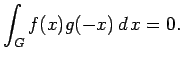
![]() as the weak-* limit of
trigonometric polynomials,
as the weak-* limit of
trigonometric polynomials,
![]() ,
with characters in
,
with characters in ![]() . Then
. Then
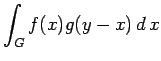
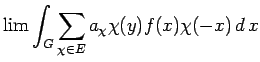
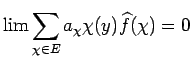
![]() is not 0 a.e..
Then, there is
is not 0 a.e..
Then, there is ![]() in
in ![]() such that
such that
![]() is not 0 a.e.. But this contradicts (i),
since
is not 0 a.e.. But this contradicts (i),
since
![]() ,
, ![]() is in
is in ![]() ,
and
,
and
![]() on
on ![]() .
.
![]() -sets, known as the
Calderón sets, or
-sets, known as the
Calderón sets, or ![]() -sets,
is particularly useful to us.
These are defined as follows.
A subset
-sets,
is particularly useful to us.
These are defined as follows.
A subset ![]() of
of ![]() is
called a
is
called a ![]() -set if every
-set if every ![]() in
in
![]() with Fourier transform
vanishing on
with Fourier transform
vanishing on ![]() can be approximated
in the
can be approximated
in the ![]() -norm by functions of the
form
-norm by functions of the
form ![]() where
where
![]() and
and
![]() vanishes on
an open set containing
vanishes on
an open set containing ![]() .
.
![]() -sets enjoy the following properties
(see [21, (39.39)] or [22, Section 7.5]).
-sets enjoy the following properties
(see [21, (39.39)] or [22, Section 7.5]).
![]() -sets, we conclude that
-sets, we conclude that
![]() ,
and
,
and ![]() , for all
, for all ![]() ,
are
,
are ![]() -sets.
>From the definition of
-sets.
>From the definition of
![]() , (13),
and the fact that
, (13),
and the fact that
![]() is open and closed, it
follows that the boundary of
is open and closed, it
follows that the boundary of
![]() is the
closed subgroup
is the
closed subgroup
![]() .
Hence
.
Hence
![]() is a
is a ![]() -set.
For
-set.
For
![]() , the set
, the set
![]() is open and closed,
and so it has
empty boundary, and thus it is a
is open and closed,
and so it has
empty boundary, and thus it is a ![]() -set. Likewise
-set. Likewise
![]() is a
is a ![]() -set for all
-set for all
![]() .
>From this we conclude that
arbitrary unions of
.
>From this we conclude that
arbitrary unions of ![]() and
and
![]() are
are ![]() -sets, because an arbitrary union of
such sets, not including the index
-sets, because an arbitrary union of
such sets, not including the index ![]() , is open and closed,
and so it is a
, is open and closed,
and so it is a ![]() -set.
-set.
![]() , and any
, and any
![]() , we have
, we have
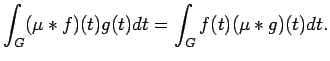
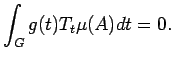
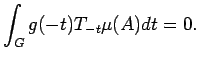
![]() functions
similar to the characterization of
functions
similar to the characterization of ![]() functions which are
constant on cosets of a subgroup [21, Theorem (28.55)].
functions which are
constant on cosets of a subgroup [21, Theorem (28.55)].
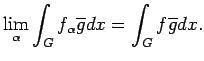
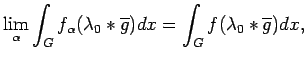
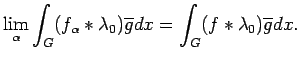
![]() to denote the
normalized Haar measure on the compact subgroup
to denote the
normalized Haar measure on the compact subgroup
![]() , the annihilator in
, the annihilator in ![]() of
of ![]() .
This measure is also characterized by its Fourier
transform:
.
This measure is also characterized by its Fourier
transform: