We continue with the notation of the previous section:
![]() is a locally compact abelian group,
is a locally compact abelian group,
![]() the dual group of
the dual group of ![]() ,
, ![]() is a measurable
order on
is a measurable
order on ![]() ,
, ![]() is a sup path
attaining representation of
is a sup path
attaining representation of ![]() acting on
acting on ![]() .
Associated with
.
Associated with ![]() is a collection of homomorphisms
is a collection of homomorphisms
![]() , as described by Theorem 2.1. Let
, as described by Theorem 2.1. Let
![]() denote the
adjoint of
denote the
adjoint of
![]() . Thus,
. Thus,
![]() is a continuous
homomorphism of
is a continuous
homomorphism of ![]() into
into ![]() .
By composing the representation
.
By composing the representation ![]() with the
with the
![]() , we define a new representation
, we define a new representation
![]() of
of ![]() acting on
acting on ![]() by:
by:
![]() . If
. If ![]() in
in ![]() is weakly measurable with respect to
is weakly measurable with respect to ![]() then
then ![]() is also weakly measurable with respect
to
is also weakly measurable with respect
to
![]() . We will further suppose that
. We will further suppose that
![]() is sup path attaining for each
is sup path attaining for each ![]() . This is the case with the representations
of Example 1.7.
. This is the case with the representations
of Example 1.7.
Our goal in this section is to relate the notion of
analyticity with respect to ![]() to the
notion of analyticity with respect to
to the
notion of analyticity with respect to
![]() .
More generally,
suppose that
.
More generally,
suppose that ![]() and
and ![]() are two
locally compact abelian groups with dual groups
are two
locally compact abelian groups with dual groups ![]() and
and
![]() , respectively. Let
, respectively. Let
Our first result is a very useful fact from spectral synthesis of bounded functions. The proof uses in a crucial way the fact that the representation is sup path attaining, or, more precisely, satisfies the property in Proposition 1.4.
Proof. Since ![]() is an
is an ![]() -subset of
-subset of ![]() , it is enough to show that for every
`
, it is enough to show that for every
`
![]() ,
,
![]() , by
Proposition 3.7.
For this purpose, it is enough by
[21, Theorem (40.8)], to show that
, by
Proposition 3.7.
For this purpose, it is enough by
[21, Theorem (40.8)], to show that
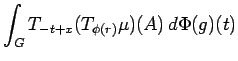 | |||
| 0 |
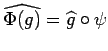 and so
and so
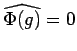 on
on
Given ![]() , a collection of elements in
, a collection of elements in
![]() or
or ![]() , let
, let
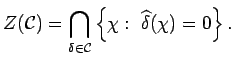
Proof. It is enough to establish the first equality; the second one follows from definitions.
We have
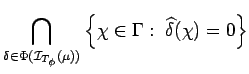 | |||
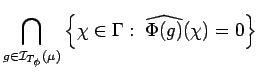 | |||
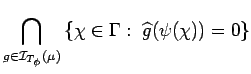 | |||
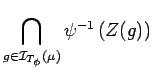 | |||
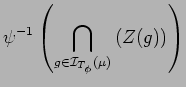 | |||
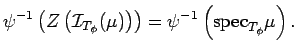 |
Proof.
We will use the notation of Lemma 4.2.
If
![]() and
and ![]() ,
then
,
then
![]() . So,
for
. So,
for
![]() , we have
, we have
![]() .
But
.
But
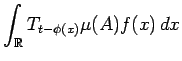 | |||
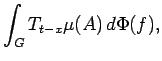 |
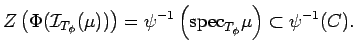
Taking
![]() and
and
![]() to be one of the
homomorphisms in Theorem 2.1,
and using the fact that
to be one of the
homomorphisms in Theorem 2.1,
and using the fact that
![]() ,
, ![]() ,
,
![]() are all
are all ![]() -sets,
we obtain useful relationships between different
types of analyticity.
-sets,
we obtain useful relationships between different
types of analyticity.
We can use the representation ![]() to convolve a measure
to convolve a measure
![]() with
with
![]() :
:
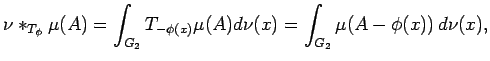
Alternatively, we can convolve
![]() in the usual sense of [20, Definition 19.8]
with
in the usual sense of [20, Definition 19.8]
with ![]() to yield
another measure in
to yield
another measure in ![]() , defined on the Borel subsets of
, defined on the Borel subsets of ![]() by
by
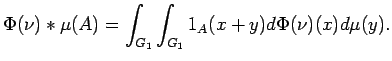
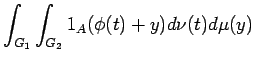 | |||
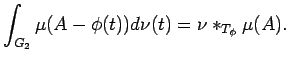 |
Proof. We have
![]() .
Also
.
Also
![]() is a
is a ![]() -set.
So (27) will follow from Theorem
1.8
once we show that
-set.
So (27) will follow from Theorem
1.8
once we show that
![]() . For that purpose, we use Lemma 4.1.
We have
. For that purpose, we use Lemma 4.1.
We have
The following special case of Theorem 4.5 deserves a separate statement.
Proof. The proof is very much like the
proof of Theorem 4.5.
We have
![]() .
Apply Theorem 1.8, taking into consideration that
.
Apply Theorem 1.8, taking into consideration that