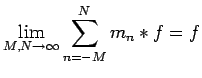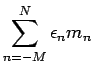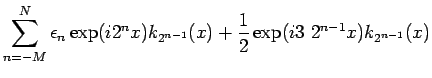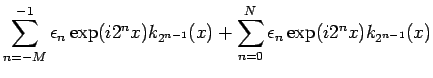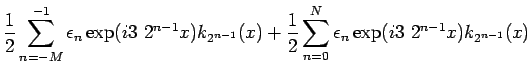Next: Bibliography
Up: Transference in Spaces of
Previous: Proof of the Main
In the remainder of this paper,
we transfer a result from Littlewood-Paley theory in
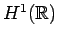 to spaces of measures on which
to spaces of measures on which
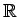 is acting.
We then show
how this transferred result implies
with ease several of the main results of Bochner [3],
de Leeuw and Glicksberg [6], and Forelli [9].
is acting.
We then show
how this transferred result implies
with ease several of the main results of Bochner [3],
de Leeuw and Glicksberg [6], and Forelli [9].
We start by setting our notation. Let
Let
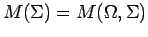 denote a space of measures and
let
denote a space of measures and
let
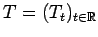 denote a sup path attaining representation of
denote a sup path attaining representation of
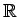 by isomorphisms of
by isomorphisms of 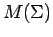 .
According to Forelli [9],
a measure
.
According to Forelli [9],
a measure
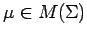 is called
is called  -analytic if
-analytic if
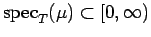 .
We now introduce another equivalent definition.
.
We now introduce another equivalent definition.
Definition 4.1
Suppose that  is a sup path attaining representation of
is a sup path attaining representation of
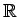 by isomorphisms of
by isomorphisms of 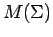 . A measure
. A measure
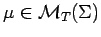 is
called weakly analytic if the mapping
is
called weakly analytic if the mapping
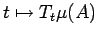 is in
is in
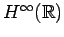 for every
for every
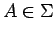 .
.
It is easy to see that if 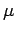 is
is  -analytic then it is
weakly analytic. The converse is also true. The proof is based on the
fact that
-analytic then it is
weakly analytic. The converse is also true. The proof is based on the
fact that
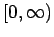 is a set of spectral synthesis (see [1, Proposition 1.7]).
is a set of spectral synthesis (see [1, Proposition 1.7]).
For
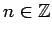 ,
let
,
let
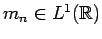 be the function whose Fourier
transform is piecewise linear and satisfies
be the function whose Fourier
transform is piecewise linear and satisfies
![$\displaystyle \widehat{m_n}(s)=\left\{ \begin{array}{ll} 0 & \mbox{if $s\not\in [2^{n-1},2^{n+1}]$;}\\ 1 & \mbox{if $s=2^n$.} \end{array} \right.$](img265.png) |
(22) |
Let
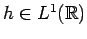 be the function whose Fourier transform is piecewise
linear and satisfies
be the function whose Fourier transform is piecewise
linear and satisfies
![$\displaystyle \widehat{h}(s)=\left\{ \begin{array}{ll} 0 & \mbox{if $s\not\in [-1,1]$,}\\ 1 & \mbox{if $\vert s\vert\leq \frac{1}{2}$.} \end{array} \right.$](img267.png) |
(23) |
It is easy to check that
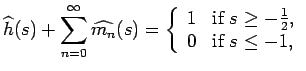 |
(24) |
and that the left side of
(24) is continuous and piecewise linear.
The following theorem is a consequence of
standard facts from Littlewood-Paley theory.
We postpone its proof to the end of this section.
Our main theorem is the following.
Proof. To prove (27),
combine Theorems 1.6 and 4.2.
Inequality (27) states that the partial sums of the series
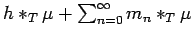 are unconditionally bounded.
To prove that they converge unconditionally, we recall
the Bessaga-Pe
are unconditionally bounded.
To prove that they converge unconditionally, we recall
the Bessaga-Pe czynski Theorem from [2]. This theorem
tells us that for any Banach
space, every unconditionally bounded series is
unconditionally convergent if and
only if the Banach space does not contain an isomorphic copy of
czynski Theorem from [2]. This theorem
tells us that for any Banach
space, every unconditionally bounded series is
unconditionally convergent if and
only if the Banach space does not contain an isomorphic copy of  .
Now since
.
Now since
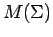 is weakly complete and
is weakly complete and 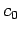 is not
(see [7, Chap IV.9, Theorem 3, and IV.13.9]), we conclude that
is not
(see [7, Chap IV.9, Theorem 3, and IV.13.9]), we conclude that
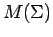 does not contain
does not contain 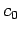 .
Applying the Bessaga-Pe
.
Applying the Bessaga-Pe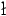 czynski Theorem, we infer that there is a measure
czynski Theorem, we infer that there is a measure
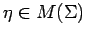 such that
such that
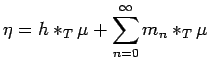 |
(29) |
unconditionally in 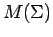 . Moreover,
. Moreover, 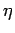 is weakly measurable,
because of (29).
It remains to show that
is weakly measurable,
because of (29).
It remains to show that 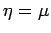 .
By Proposition 2.4,
it is enough to show that
for every
.
By Proposition 2.4,
it is enough to show that
for every
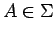 , we have
, we have
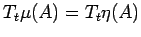 |
(30) |
for almost every
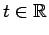 .
Since
.
Since 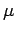 is weakly analytic, the function
is weakly analytic, the function
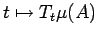 is in
is in
 .
By Theorem 4.2 (iii),
we have
.
By Theorem 4.2 (iii),
we have
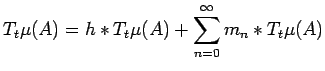 |
(31) |
for almost every
 . On the other hand, from
the unconditional convergence of the series in
(29), (1), and (3), it
follows that
. On the other hand, from
the unconditional convergence of the series in
(29), (1), and (3), it
follows that
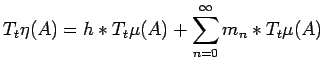 |
(32) |
for all
 . Comparing (31) and
(32), we see that (30)
holds, completing the proof of the theorem.
. Comparing (31) and
(32), we see that (30)
holds, completing the proof of the theorem.
Remarks 4.4 It is interesting to note that
Theorem
4.3
implies the classical
F. and M. Riesz theorem for measures defined on the real line.
To see this, consider the representation
of
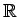
acting by translation on the Banach space
of complex regular
Borel measures on
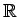
.
It is easy to see that a regular Borel measure is analytic
if and only if its Fourier-Stieltjes transform is supported in
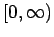
.
In this case, each term in
(
28) belongs to
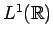
,
being the convolution of an
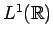
function with a regular Borel measure.
Thus, the unconditional convergence of the
series in (
28) implies that the
measure
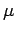
is absolutely continuous.
This argument provides a
new proof of the F. and M. Riesz Theorem,
based on Littlewood-Paley theory and the result of
Bessaga-Pe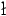 czynski [2]. Also, it can be used to
prove the following version of Bochner's generalization of the F. and M. Riesz Theorem.
czynski [2]. Also, it can be used to
prove the following version of Bochner's generalization of the F. and M. Riesz Theorem.
Theorem 4.5
Suppose that 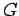 is a locally compact abelian group with
dual group
is a locally compact abelian group with
dual group 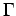 , and
, and
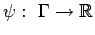 is a
continuous homomorphism. Suppose that
is a
continuous homomorphism. Suppose that
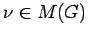 is such that,
for every real number
is such that,
for every real number 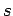 ,
,
![$ \psi^{-1}((-\infty,s])\cap {\rm supp}(\widehat{\nu})$](img294.png) is compact.
Then
is compact.
Then 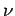 is absolutely continuous with
respect to Haar measure on
is absolutely continuous with
respect to Haar measure on 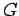 . That is,
. That is,
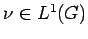 .
.
Proof.
Let
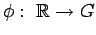 denote the continuous adjoint homomorphism
of
denote the continuous adjoint homomorphism
of 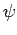 . Define a representation
. Define a representation
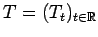 of
of
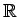 on
the regular Borel measures
on
the regular Borel measures 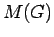 by
for all
by
for all
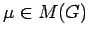 and all Borel subsets
and all Borel subsets
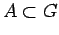 .
By Example 2.2,
.
By Example 2.2,  is sup path attaining,
and every measure
is sup path attaining,
and every measure
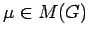 is weakly measurable.
Moreover,
is weakly measurable.
Moreover,
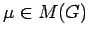 is weakly analytic (equivalently,
is weakly analytic (equivalently,  -analytic)
if and only if
-analytic)
if and only if
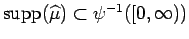 (see
[6]).
(see
[6]).
To prove the theorem, we can, without loss of generality,
suppose that
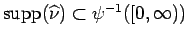 .
Otherwise, we consider the measure
.
Otherwise, we consider the measure
 , where
, where
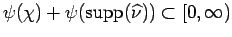 .
.
Let
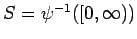 . Then
. Then 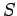 is a
is a 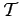 -set. Applying Theorem 4.3, we see that
-set. Applying Theorem 4.3, we see that
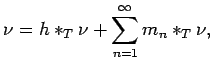 |
(33) |
unconditionally in  .
For
.
For
 , a
straightforward calculation shows that
, a
straightforward calculation shows that
 for all
for all
 .
Since
.
Since
![$ \psi^{-1}((-\infty,s])\cap {\rm supp}(\widehat{\nu})$](img294.png) is compact
for every
is compact
for every
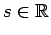 , it follows that
, it follows that
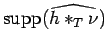 and
and
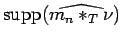 are compact. Thus
are compact. Thus 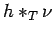 and
and 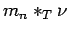 are in
are in
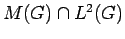 , and hence they belong to
, and hence they belong to 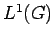 .
As a consequence, (33) implies that
.
As a consequence, (33) implies that
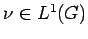 .
.
With Theorem 4.3 in hand, we can derive with ease
several fundamental properties of analytic measures
that were obtained previously by
de Leeuw-Glicksberg
[6], and
Forelli [9]. We note however, that the techniques
in [6] and [9] do not apply
in our more general settings.
Theorem 4.6
Let  be a representation of
be a representation of
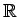 in
in 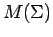 that is sup path attaining,
and let
that is sup path attaining,
and let 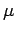 be a
weakly analytic measure in
be a
weakly analytic measure in 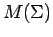 .
Then the mapping
.
Then the mapping
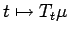 is
continuous from
is
continuous from
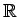 into
into 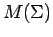 .
.
Proof. Using the uniform continuity
of translation in
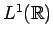 , it is a simple matter to show that
for any function
, it is a simple matter to show that
for any function
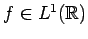 , and any weakly measurable
, and any weakly measurable
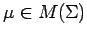 , the mapping
, the mapping
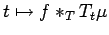 is continuous.
Now use Theorem 4.3 to complete the proof.
is continuous.
Now use Theorem 4.3 to complete the proof.
Theorem 4.6 is very specific to
representations of
 or
or
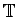 , in the sense that
no similar result holds on more general groups.
To see this, consider the
group
, in the sense that
no similar result holds on more general groups.
To see this, consider the
group
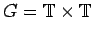 with a lexicographic order on the dual
group
with a lexicographic order on the dual
group
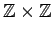 . Let
. Let 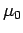 denote the normalized Haar
measure on the subgroup
denote the normalized Haar
measure on the subgroup
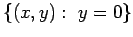 , and consider the measure
, and consider the measure
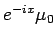 . Its spectrum is supported on
the coset
. Its spectrum is supported on
the coset
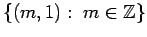 and thus it is
analytic with respect to the
regular action of
and thus it is
analytic with respect to the
regular action of 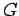 by translation in
by translation in
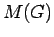 . Clearly, the measure
. Clearly, the measure
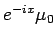 does not translate continuously, and so
a straightforward analog of
Theorem 4.6
fails in this setting.
does not translate continuously, and so
a straightforward analog of
Theorem 4.6
fails in this setting.
The following application concerns bounded operators  from
from 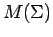 into
into 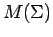 that commute with
that commute with  in the following sense:
in the following sense:
for all
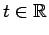 .
.
Theorem 4.7
Suppose that  is a representation of
is a representation of
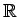 that is sup path
attaining,
and that
that is sup path
attaining,
and that  commutes with
commutes with  .
Let
.
Let
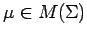 be weakly analytic.
Then
be weakly analytic.
Then
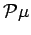 is also weakly analytic.
is also weakly analytic.
Proof.
First note that by Theorem 4.6, the mapping
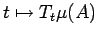 is continuous, and hence measurable.
is continuous, and hence measurable.
Now suppose that
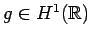 . Again, by Theorem 4.6,
the
map
. Again, by Theorem 4.6,
the
map
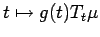 is Bochner integrable.
Let
is Bochner integrable.
Let
Then by properties of the Bochner integral,
and since 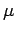 is weakly analytic, we have that
for all
is weakly analytic, we have that
for all
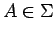 Hence
Hence 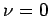 .
Therefore, for all
.
Therefore, for all
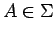 we have
Since this is true for all
we have
Since this is true for all
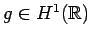 , it follows that
, it follows that
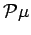 is weakly analytic.
is weakly analytic.
Definition 4.8
Let  be a sup path attaining
representation of
be a sup path attaining
representation of 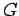 in
in 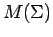 .
A weakly measurable
.
A weakly measurable 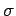 in
in 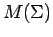 is
called quasi-invariant if
is
called quasi-invariant if
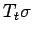 and
and 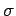 are mutually absolutely continuous for all
are mutually absolutely continuous for all 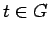 . Hence
if
. Hence
if 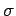 is quasi-invariant
and
is quasi-invariant
and
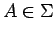 , then
, then
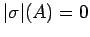 if and only if
if and only if
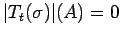 for all
for all 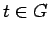 .
.
We can use Theorem 4.7 to generalize a result of
de Leeuw-Glicksberg [6]
and Forelli [9], concerning quasi-invariant measures. In this application, it
is necessary to restrict
to sup path attaining representations given by isometries of 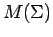 .
We need a lemma.
.
We need a lemma.
Lemma 4.9
Suppose that  is a linear isometry of
is a linear isometry of 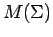 onto itself.
Let
onto itself.
Let 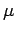 ,
,
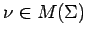 . Then,
. Then,
(a) 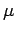 and
and 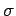 are mutually singular (in symbols,
are mutually singular (in symbols,
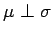 )
if and only if
)
if and only if
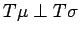 ;
;
(b)
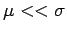 if and only if
if and only if
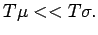
Proof. For (a), simply recall that two measures 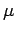 and
and 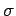 are mutually singular if and only if
are mutually singular if and only if
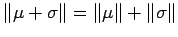 , and
, and
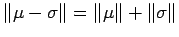 .
For (b), it is clearly enough to prove the implication in one direction.
So suppose that
.
For (b), it is clearly enough to prove the implication in one direction.
So suppose that
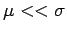 and write
and write
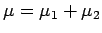 where
where
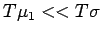 and
and
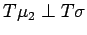 .
Then
.
Then
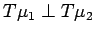 . Hence
. Hence
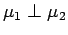 , and hence
, and hence
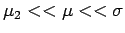 .
But
.
But
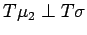 implies that
implies that
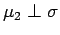 . So
. So
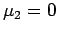 . Thus
. Thus
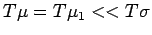 .
.
Theorem 4.10
Suppose that  is a sup path attaining representation
of
is a sup path attaining representation
of
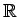 by isometries of
by isometries of 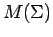 . Suppose
that
. Suppose
that
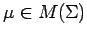 is weakly analytic, and
is weakly analytic, and
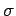 is quasi-invariant. Write
is quasi-invariant. Write
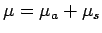 for the Lebesgue decomposition of
for the Lebesgue decomposition of 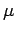 with respect to
with respect to 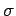 . Then both
. Then both
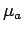 and
and 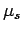 are weakly analytic. In particular,
the spectra of
are weakly analytic. In particular,
the spectra of 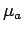 and
and 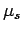 are
contained in
are
contained in
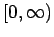 .
.
Proof. Let
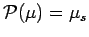 .
Since
.
Since 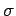 is quasi-invariant, the operator
is quasi-invariant, the operator
 commutes with
commutes with  by Lemma 4.9.
Now apply Theorem
4.7.
by Lemma 4.9.
Now apply Theorem
4.7.
Let us finish with an example to show that the hypothesis of
sup path attaining is required in these results. The
next example is a variant of Example 2.5.
Example 4.11 Let
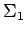
denote the sigma algebra of countable
and co-countable subsets of
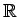
, let
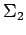
denote
the Borel subsets of
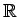
, and let
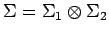
denote the product sigma algebra on
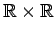
.
Let
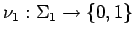
be the measure that takes countable sets
to 0 and co-countable sets to
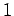
, let
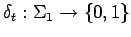
be the measure that takes sets to
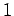
if they contain
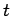
, and to 0 otherwise,
and let
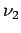
denote the measure on
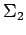
given by
Let
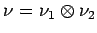
,
let
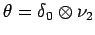
, and
let
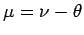
.
Finally, let
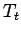
be the representation given by
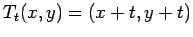
.
Then, we see that  is quasi-invariant, and that
is quasi-invariant, and that
 and
and 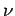 are mutually singular.
Arguing as in
Example 2.5, we see that
are mutually singular.
Arguing as in
Example 2.5, we see that 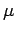 is weakly analytic.
However, the singular part of
is weakly analytic.
However, the singular part of 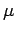 with respect to
with respect to 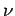 is
is 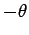 , and it may be readily seen that this is
not weakly analytic, for example
, and it may be readily seen that this is
not weakly analytic, for example
is not in
.
We end this section by proving Theorem 4.2.
We have
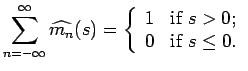 |
(34) |
Recall the Fejér kernels
 , where
, where
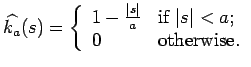 |
(35) |
By Fourier inversion, we see that
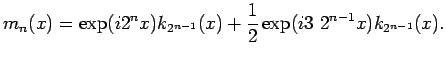 |
(36) |
Proof.
The proof of (ii) is immediate from (i) and (34),
by Fourier inversion.
For part (i),
use (36),
to write
Hence, to prove (37)
it is enough to show that there is a positive constant
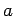 , independent of
, independent of 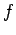 such that
such that
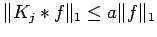 , for
, for 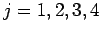 .
Appealing to [15, Theorem 3, p. 114], we will be done once we
establish that:
.
Appealing to [15, Theorem 3, p. 114], we will be done once we
establish that:
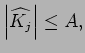 |
(38) |
and the Hörmander condition
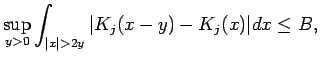 |
(39) |
where 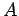 and
and 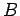 are absolute constants.
Inequality (38)
holds with
are absolute constants.
Inequality (38)
holds with 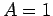 , since the
Fourier transforms of the summands defining the
kernels
, since the
Fourier transforms of the summands defining the
kernels 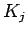 have disjoint supports and are
bounded by 1. Condition (39), is well-known.
For a proof, see [8, pp. 138-140, and 7.2.2, p. 142].
have disjoint supports and are
bounded by 1. Condition (39), is well-known.
For a proof, see [8, pp. 138-140, and 7.2.2, p. 142].
Proof of Theorem 4.2.
Parts (i) and (ii) follow
as in Theorem 4.12,
so we only prove (iii).
For notational convenience, let
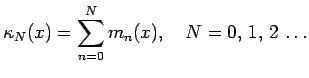 |
(40) |
Let 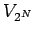 denote the de la Vallée
Poussin kernels on
denote the de la Vallée
Poussin kernels on
 of order
of order  .
Its Fourier transform is
continuous, piecewise linear,
and satisfies
.
Its Fourier transform is
continuous, piecewise linear,
and satisfies
![$\displaystyle \widehat{V_{2^N}}(s)=\left\{ \begin{array}{ll} 0 & \mbox{if $s\no...
...2^{n+1},2^{n+1}]$;}\\ 1 & \mbox{if $\vert s\vert\leq 2^n$.} \end{array} \right.$](img392.png) |
(41) |
It is well-known that 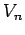 is a summability kernel for
is a summability kernel for
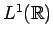 and, in particular, that
and, in particular, that 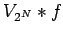 converges pointwise almost everywhere to
converges pointwise almost everywhere to 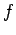 for all
for all
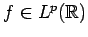 , for
, for
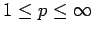 .
Thus, we will be done, if we can show that for
.
Thus, we will be done, if we can show that for
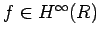 ,
,
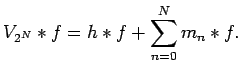 |
(42) |
Write
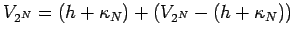 ,
where
,
where 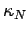 is as in (40).
For
is as in (40).
For 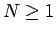 , the Fourier transform of
, the Fourier transform of
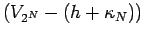 ,
vanishes on
,
vanishes on
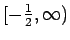 .
Thus, for
.
Thus, for
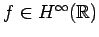 , we have
, we have
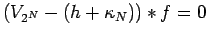 , and so
(42) follows, and the proof
is complete.
, and so
(42) follows, and the proof
is complete.
Acknowledgements The work of the second author was supported
by a grant from the National Science Foundation (U.S.A.).



Next: Bibliography
Up: Transference in Spaces of
Previous: Proof of the Main
Stephen Montgomery-Smith
2002-10-30
![]() to spaces of measures on which
to spaces of measures on which
![]() is acting.
We then show
how this transferred result implies
with ease several of the main results of Bochner [3],
de Leeuw and Glicksberg [6], and Forelli [9].
is acting.
We then show
how this transferred result implies
with ease several of the main results of Bochner [3],
de Leeuw and Glicksberg [6], and Forelli [9].
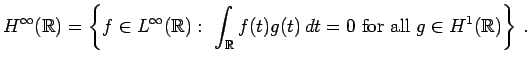
![]() ,
let
,
let
![]() be the function whose Fourier
transform is piecewise linear and satisfies
be the function whose Fourier
transform is piecewise linear and satisfies
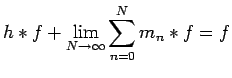
![]() are unconditionally bounded.
To prove that they converge unconditionally, we recall
the Bessaga-Pe
are unconditionally bounded.
To prove that they converge unconditionally, we recall
the Bessaga-Pe![]() czynski Theorem from [2]. This theorem
tells us that for any Banach
space, every unconditionally bounded series is
unconditionally convergent if and
only if the Banach space does not contain an isomorphic copy of
czynski Theorem from [2]. This theorem
tells us that for any Banach
space, every unconditionally bounded series is
unconditionally convergent if and
only if the Banach space does not contain an isomorphic copy of ![]() .
Now since
.
Now since
![]() is weakly complete and
is weakly complete and ![]() is not
(see [7, Chap IV.9, Theorem 3, and IV.13.9]), we conclude that
is not
(see [7, Chap IV.9, Theorem 3, and IV.13.9]), we conclude that
![]() does not contain
does not contain ![]() .
Applying the Bessaga-Pe
.
Applying the Bessaga-Pe![]() czynski Theorem, we infer that there is a measure
czynski Theorem, we infer that there is a measure
![]() such that
such that
![]() czynski [2]. Also, it can be used to
prove the following version of Bochner's generalization of the F. and M. Riesz Theorem.
czynski [2]. Also, it can be used to
prove the following version of Bochner's generalization of the F. and M. Riesz Theorem.
![]() .
Otherwise, we consider the measure
.
Otherwise, we consider the measure
![]() , where
, where
![]() .
.
![]() . Then
. Then ![]() is a
is a ![]() -set. Applying Theorem 4.3, we see that
-set. Applying Theorem 4.3, we see that
![]() or
or
![]() , in the sense that
no similar result holds on more general groups.
To see this, consider the
group
, in the sense that
no similar result holds on more general groups.
To see this, consider the
group
![]() with a lexicographic order on the dual
group
with a lexicographic order on the dual
group
![]() . Let
. Let ![]() denote the normalized Haar
measure on the subgroup
denote the normalized Haar
measure on the subgroup
![]() , and consider the measure
, and consider the measure
![]() . Its spectrum is supported on
the coset
. Its spectrum is supported on
the coset
![]() and thus it is
analytic with respect to the
regular action of
and thus it is
analytic with respect to the
regular action of ![]() by translation in
by translation in
![]() . Clearly, the measure
. Clearly, the measure
![]() does not translate continuously, and so
a straightforward analog of
Theorem 4.6
fails in this setting.
does not translate continuously, and so
a straightforward analog of
Theorem 4.6
fails in this setting.
![]() from
from ![]() into
into ![]() that commute with
that commute with ![]() in the following sense:
in the following sense:
![]() . Again, by Theorem 4.6,
the
map
. Again, by Theorem 4.6,
the
map
![]() is Bochner integrable.
Let
is Bochner integrable.
Let
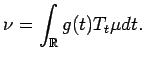
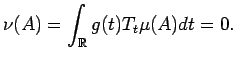
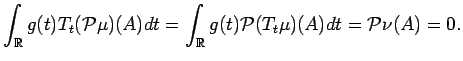
![]() .
We need a lemma.
.
We need a lemma.
![]() and
and ![]() are mutually singular if and only if
are mutually singular if and only if
![]() , and
, and
![]() .
For (b), it is clearly enough to prove the implication in one direction.
So suppose that
.
For (b), it is clearly enough to prove the implication in one direction.
So suppose that
![]() and write
and write
![]() where
where
![]() and
and
![]() .
Then
.
Then
![]() . Hence
. Hence
![]() , and hence
, and hence
![]() .
But
.
But
![]() implies that
implies that
![]() . So
. So
![]() . Thus
. Thus
![]() .
.
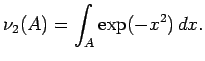
![]() is quasi-invariant, and that
is quasi-invariant, and that
![]() and
and ![]() are mutually singular.
Arguing as in
Example 2.5, we see that
are mutually singular.
Arguing as in
Example 2.5, we see that ![]() is weakly analytic.
However, the singular part of
is weakly analytic.
However, the singular part of ![]() with respect to
with respect to ![]() is
is ![]() , and it may be readily seen that this is
not weakly analytic, for example
, and it may be readily seen that this is
not weakly analytic, for example
![% latex2html id marker 4962
$\displaystyle T_t\theta(\mathbb{R}\times[-1,1])
= \int_{-1}^1 \exp(-(x-t)^2) \, dx ,$](img368.png)