


Next: Transference in Spaces of
Up: Transference in Spaces of
Previous: Sup Path Attaining Representations
Throughout this section, 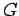 denotes a locally compact abelian group with dual group
denotes a locally compact abelian group with dual group 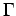 ;
; 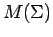 is a space of measures on a set
is a space of measures on a set
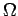 ; and
; and
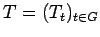 is a sup path attaining representation of
is a sup path attaining representation of 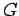 by isomorphisms of
by isomorphisms of 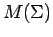 .
.
If
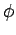 is in
is in
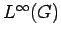 , write
, write
![$ \left[ \phi\right]$](img161.png) for the smallest weak-* closed translation-invariant subspace of
for the smallest weak-* closed translation-invariant subspace of
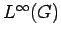 containing
containing 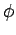 , and let
, and let
![$ {\cal I}([\phi])={\cal I}(\phi)$](img162.png) denote the closed translation-invariant ideal in
denote the closed translation-invariant ideal in 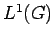 :
:
It is clear that
![$ {\cal I}(\phi)=\{f\in L^1(G): f*g=0, \forall g\in \left[\phi\right]\}$](img164.png) .
The spectrum of
.
The spectrum of 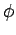 , denoted by
, denoted by
![$ \sigma \left[\phi\right]$](img165.png) ,
is the set of all continuous characters of
,
is the set of all continuous characters of 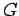 that belong to
that belong to
![$ \left[ \phi\right]$](img161.png) .
This closed subset of
.
This closed subset of 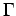 is also given by
is also given by
![$\displaystyle \sigma \left[\phi\right]=Z({\cal I}(\phi)).$](img166.png) |
(13) |
(See [14, Chapter 7, Theorem 7.8.2, (b), (c), and (d)].)
Remarks 3.1 (a) For a weakly measurable
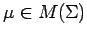
, since
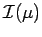
is a closed ideal
in
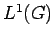
, it is translation-invariant, by
[
14, Theorem 7.1.2].
It follows readily that
for all
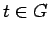
,
and hence
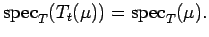 |
(14) |
(b) Let
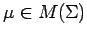
be weakly measurable and let
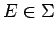
.
It is clear that
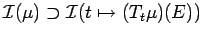
. Thus
![$ \sigma\left[ t\mapsto (T_t\mu)(E)\right]\subset {\rm spec}_T(\mu)$](img171.png)
.
Proof. (a) Fix
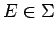 and
and
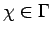 , and let
, and let
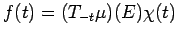 .
Then
.
Then
![$ \sigma\left[ f\right]\subset \chi -{\rm spec}_T(\mu)$](img181.png) .
Hence, for
.
Hence, for
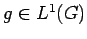 with
supp
with
supp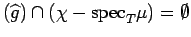 ,
we have
(b) Immediate from
,
we have
(b) Immediate from
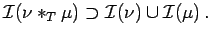
(c) Fix  on
on  with
with  and let
and let
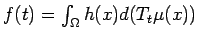 . Then
. Then
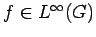 and so, if
and so, if
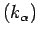 is an approximate
identity for
is an approximate
identity for 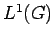 , then
, then
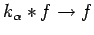 in the weak
in the weak 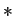 -topology of
-topology of
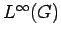 . Hence
. Hence
The proof is completed by taking the sup of
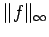 over all
over all 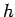 and using (7).
and using (7).
Proof. We suppose throughout the proof that
the right side of (15) is finite; otherwise there is nothing to prove.
Write
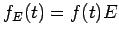 . Thus
is continuous on
. Thus
is continuous on 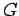 . By (i) and (ii),
. By (i) and (ii),
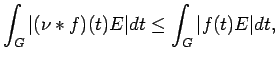 |
(16) |
for all
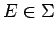 . Now let
. Now let 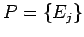 be a finite measurable partition of
be a finite measurable partition of
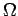 , and define
Then
, and define
Then
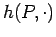 is continuous on
is continuous on 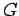 and, by (16),
and, by (16),
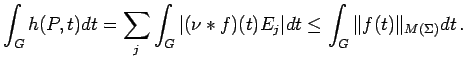 |
(17) |
If 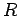 is a common refinement of
is a common refinement of 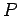 and
and 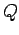 , then, for all
, then, for all 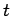 ,
It follows from [12, (11.13)] that
,
It follows from [12, (11.13)] that
by (17).
Proof of Theorem 1.6.
Let
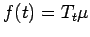 and suppose first that
and suppose first that
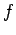 is continuous and that there is a neighborhood
is continuous and that there is a neighborhood 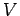 of
of
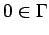 such that
such that
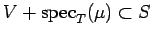 .
Choose a continuous
.
Choose a continuous
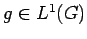 such that
such that
and
Then, for all
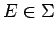 , the mapping
, the mapping
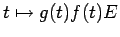 is bounded and continuous on
is bounded and continuous on 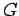 , and, by Lemma 3.2,
belongs to
Hence Lemma 3.3 implies that
, and, by Lemma 3.2,
belongs to
Hence Lemma 3.3 implies that
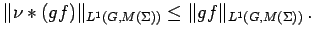 |
(18) |
We now proceed to show that (10) is
a consequence of (18).
We start with the right side of (18):
Consider now the left side of (18). We have
Inequalities (18), (19), and (20) imply that
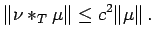 |
(21) |
Now fix
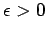 and let
and let
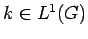 be such that
be such that
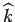 has compact support in
has compact support in 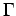 .
We have by Lemma 3.2
.
We have by Lemma 3.2
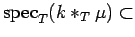
supp
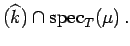
Moreover, the set
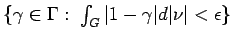 is a neighborhood of
is a neighborhood of
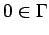 . Hence, by the hypothesis on
. Hence, by the hypothesis on 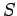 ,
there is a neighborhood
,
there is a neighborhood 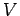 of 0 in
of 0 in 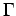 and
and
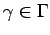 such that
such that
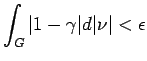
and
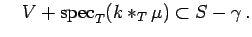
If
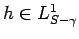 , then
, then
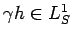 ; hence
for all
; hence
for all
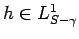 .
Since translation in
.
Since translation in 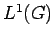 is continuous, it follows that
the map
is continuous, it follows that
the map
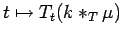 is continuous, and hence we obtain
from (21),
As
is continuous, and hence we obtain
from (21),
As
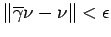 and
and 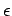 is arbitrary, we
get
Letting
is arbitrary, we
get
Letting 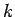 run through an approximate identity of
run through an approximate identity of 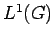 and using
Lemma 3.2, we obtain
and using
Lemma 3.2, we obtain
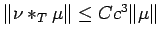 .
.



Next: Transference in Spaces of
Up: Transference in Spaces of
Previous: Sup Path Attaining Representations
Stephen Montgomery-Smith
2002-10-30
![]() denotes a locally compact abelian group with dual group
denotes a locally compact abelian group with dual group ![]() ;
; ![]() is a space of measures on a set
is a space of measures on a set
![]() ; and
; and
![]() is a sup path attaining representation of
is a sup path attaining representation of ![]() by isomorphisms of
by isomorphisms of ![]() .
.
![]() is in
is in
![]() , write
, write
![]() for the smallest weak-* closed translation-invariant subspace of
for the smallest weak-* closed translation-invariant subspace of
![]() containing
containing ![]() , and let
, and let
![]() denote the closed translation-invariant ideal in
denote the closed translation-invariant ideal in ![]() :
:
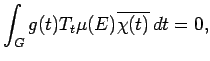
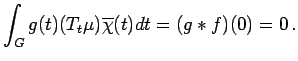
![]() on
on ![]() with
with ![]() and let
and let
![]() . Then
. Then
![]() and so, if
and so, if
![]() is an approximate
identity for
is an approximate
identity for ![]() , then
, then
![]() in the weak
in the weak ![]() -topology of
-topology of
![]() . Hence
. Hence
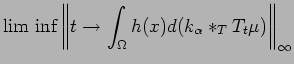
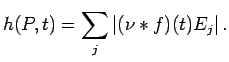
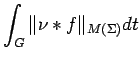
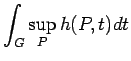
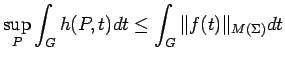
![]() and suppose first that
and suppose first that
![]() is continuous and that there is a neighborhood
is continuous and that there is a neighborhood ![]() of
of
![]() such that
such that
![]() .
Choose a continuous
.
Choose a continuous
![]() such that
such that
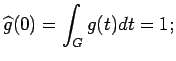
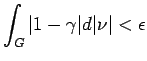 and
and