Transference theory for ![]() spaces is a powerful tool with
many fruitful applications to singular integrals, ergodic
theory, and spectral theory of operators [4,5].
These methods afford a unified approach to many problems
in diverse areas, which before were proved by a variety of methods.
spaces is a powerful tool with
many fruitful applications to singular integrals, ergodic
theory, and spectral theory of operators [4,5].
These methods afford a unified approach to many problems
in diverse areas, which before were proved by a variety of methods.
The purpose of this paper is to bring about a similar approach to spaces of measures. Our main transference result is motivated by the extensions of the classical F.&M. Riesz Theorem due to Bochner [3], Helson-Lowdenslager [10,11], de Leeuw-Glicksberg [6], Forelli [9], and others. It might seem that these extensions should all be obtainable via transference methods, and indeed, as we will show, these are exemplary illustrations of the scope of our main result.
It is not straightforward to extend the classical transference methods of Calderón, Coifman and Weiss to spaces of measures. First, their methods make use of averaging techniques and the amenability of the group of representations. The averaging techniques simply do not work with measures, and do not preserve analyticity. Secondly, and most importantly, their techniques require that the representation is strongly continuous. For spaces of measures, this last requirement would be prohibitive, even for the simplest representations such as translations. Instead, we will introduce a much weaker requirement, which we will call `sup path attaining'. By working with sup path attaining representations, we are able to prove a new transference principle with interesting applications. For example, we will show how to derive with ease generalizations of Bochner's theorem and Forelli's main result. The Helson-Lowdenslager theory, concerning representations of groups with ordered dual groups, is also within reach, but it will be treated in a separate paper.
Throughout ![]() will denote a
locally compact abelian group with dual group
will denote a
locally compact abelian group with dual group
![]() .
The symbols
.
The symbols
![]() ,
,
![]() and
and
![]() denote the integers, the real and complex numbers, respectively.
If
denote the integers, the real and complex numbers, respectively.
If ![]() is a set, we denote the indicator
function of
is a set, we denote the indicator
function of ![]() by
by ![]() .
For
.
For
![]() ,
the space of Haar measurable functions
,
the space of Haar measurable functions ![]() on
on ![]() with
with
![]() will be denoted by
will be denoted by
![]() . The space of essentially
bounded functions on
. The space of essentially
bounded functions on ![]() will be denoted by
will be denoted by
![]() . The expressions ``locally null''
and ``locally almost everywhere'' will have the same meanings as
in [12, Definition (11.26)].
. The expressions ``locally null''
and ``locally almost everywhere'' will have the same meanings as
in [12, Definition (11.26)].
Our measure theory is borrowed from
[12].
In particular, the space of all complex regular Borel measures
on ![]() ,
denoted by
,
denoted by ![]() , consists of all complex measures
arising from bounded linear functionals on
, consists of all complex measures
arising from bounded linear functionals on
![]() ,
the Banach space of continuous functions on
,
the Banach space of continuous functions on
![]() vanishing at infinity.
vanishing at infinity.
Let
![]() denote a
measurable space,
where
denote a
measurable space,
where ![]() is a set and
is a set and ![]() is a
sigma algebra of subsets of
is a
sigma algebra of subsets of ![]() . Let
. Let ![]() denote the
Banach space of complex measures on
denote the
Banach space of complex measures on ![]() with the
total variation norm, and let
with the
total variation norm, and let
![]() denote the space of measurable
bounded functions on
denote the space of measurable
bounded functions on ![]() .
.
Let
![]() denote a representation of
denote a representation of ![]() by isomorphisms of
by isomorphisms of ![]() .
We suppose that
.
We suppose that ![]() is uniformly bounded,
i.e., there is a positive constant
is uniformly bounded,
i.e., there is a positive constant ![]() such that
for all
such that
for all ![]() , we have
, we have
Given a measure
![]() and a Borel measure
and a Borel measure
![]() , we define the `convolution'
, we define the `convolution'
![]() on
on ![]() by
by
We will assume throughout this paper
that the representation ![]() commutes with the
convolution (2) in the following sense:
for each
commutes with the
convolution (2) in the following sense:
for each ![]() ,
,
We come now to a definition which is fundamental to our work.
The fact that the mapping
![]() is
measurable is a simple consequence of
the measurability of the mapping
is
measurable is a simple consequence of
the measurability of the mapping
![]() for every
for every
![]() .
.
Examples of sup path attaining representations will be presented in the following section. Proceeding toward the main result of this paper, we recall some basic definitions from spectral theory.
If ![]() is an ideal in
is an ideal in ![]() , let
, let
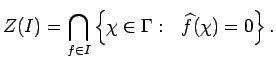
If
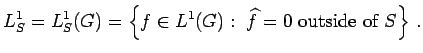
The main result of this paper is the following transference theorem.
To state Forelli's main result in [9], let us recall
two definitions of Baire sets.
Suppose that ![]() is
a topological space.
Usually,
the collection of Baire sets,
is
a topological space.
Usually,
the collection of Baire sets,
![]() , is defined
as the sigma algebra generated by sets that are compact and also countable
intersections of open sets. A second definition is to define
, is defined
as the sigma algebra generated by sets that are compact and also countable
intersections of open sets. A second definition is to define
![]() as the minimal
sigma algebra so that compactly supported continuous functions are measurable.
For locally compact Hausdorff
topological spaces, these two
definitions are equivalent.
as the minimal
sigma algebra so that compactly supported continuous functions are measurable.
For locally compact Hausdorff
topological spaces, these two
definitions are equivalent.
Suppose that
![]() is a group of
homeomorphisms
of
is a group of
homeomorphisms
of ![]() onto itself such that the mapping
onto itself such that the mapping
![]() is jointly continuous. The maps
is jointly continuous. The maps ![]() induce isomorphisms
induce isomorphisms ![]() on
the space of Baire measures via the identity
on
the space of Baire measures via the identity
![]() .
.
If ![]() is a Baire measure, we will say that it is
quasi-invariant if
is a Baire measure, we will say that it is
quasi-invariant if ![]() and
and ![]() are mutually absolutely
continuous for all
are mutually absolutely
continuous for all
![]() , that is, for all
, that is, for all
![]() we have
that
we have
that
![]() if and only if
if and only if
![]() . If
. If ![]() is
a Baire measure, we will say that
is
a Baire measure, we will say that ![]() is
is ![]() -analytic if
-analytic if
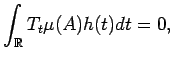
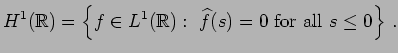
The proofs of both this result in [9], and also its predecessor
[6],
are long and difficult. Furthermore, it is hard to understand
why one must use Baire measures instead of Borel measures.
As it turns out, the mystery of why we need to use Baire measures in Forelli's work is reduced to the fact that
such representations as described above on the Baire measures are sup path attaining. By working with sup path attaining representations,
we are able to prove a more general version of Theorem 1.7.
We do not need ![]() to be locally compact Hausdorff.
Or
we might suppose that
to be locally compact Hausdorff.
Or
we might suppose that
![]() is any group of uniformly bounded
isomorphisms satisfying (3) on any Lebesgue space (that is, a
countably generated sigma algebra).
is any group of uniformly bounded
isomorphisms satisfying (3) on any Lebesgue space (that is, a
countably generated sigma algebra).