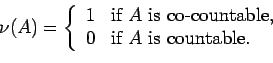Example 2.1 Let
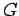
be a locally compact abelian group.
Suppose that
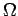
is a topological
space and
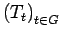
is a
group of homeomorphisms of
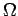
onto itself
such that the mapping
is jointly continuous.
Suppose that
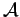
is an algebra of bounded continuous complex valued
functions
on
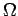
such that if
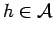
,
and if
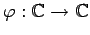
is any bounded continuous function,
and if
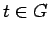
,
then
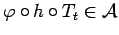
. Let
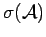
denote the
minimal sigma-algebra so that
functions from
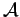
are measurable.
For any measure
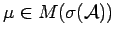
, and
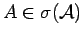
,
define
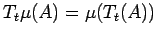
, where
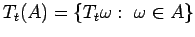
.
Note that

satisfies
(
1) and (
3).
To discuss the weak measurability of
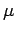
, and the sup path attaining
property of

, we need that for each
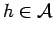
that the map
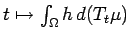
is continuous.
This
crucial property follows
for any measure
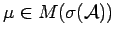
, by the dominated convergence theorem, if, for example,
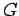
is metrizable. For arbitrary locally compact abelian groups, it is enough to require that
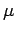
has sigma-compact support.
Henceforth, we assume that 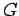 is metrizable, or that
is metrizable, or that
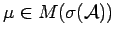 has sigma-compact support, and proceed to show that
has sigma-compact support, and proceed to show that
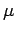 is
weakly measurable in the sense of Definition 1.1, and that
the representation
is
weakly measurable in the sense of Definition 1.1, and that
the representation  is sup path attaining.
Let
is sup path attaining.
Let
and let
Clearly,
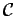
is a monotone class, closed under
nested unions and intersections. Also,
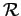
is an algebra of sets, closed under finite unions and
set complementation. Furthermore, it is clear that
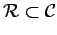
.
Hence, by the monotone class theorem,
it follows that
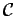
contains the
sigma algebra generated by
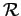
.
Now, if
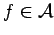
and
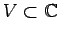
is open, then
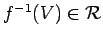
, because
Consequently, we have that
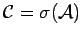
, that is,
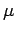
is weakly measurable.
Next, let us show that 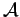 is dense in
is dense in
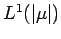 . Let
. Let
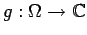 be a bounded
be a bounded
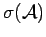 -measurable
function such that
-measurable
function such that
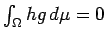 for all
for all
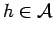 . Define
. Define 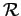 as above, and let
as above, and let
Then
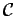
is a monotone class containing
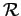
, and so arguing as
before,
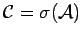
, that is,
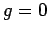
almost everywhere with respect
to
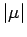
. Thus it follows by the Hahn-Banach Theorem that
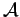
is dense in
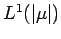
. Hence
where the last inequality follows from the fact that
the map
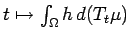
is continuous.
Hence,

is sup path attaining with
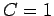
.
Example 2.3 Let
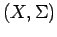
be an abstract Lebesgue
space, that is,
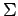
is countably generated.
Then
any uniformly bounded representation

of
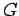
by isomorphisms of
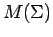
is sup path attaining.
To see this, note that since
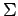
is countably
generated, there is a countable subset
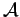
of the unit ball of
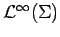
such that for any
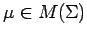
we have
If
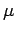
is weakly measurable, then
for
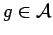
and for locally almost all
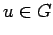
, we have
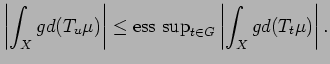 |
(12) |
Since
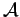
is countable we can find a subset
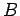
of
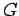
such that the complement of
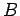
is locally null,
and such that (
12) holds for every
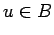
and all
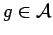
. For
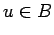
,
take the sup in (
12) over all
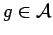
, and get
But since
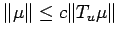
, it follows that

is sup path attaining with
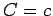
.
Sup path attaining representations satisfy the
following property, which was introduced in [1] and was
called hypothesis  .
.
Example 2.5 (a) Let
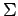
denote the sigma algebra of
countable and co-countable subsets of
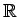
.
Define
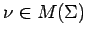
by
Let
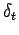
denote the point mass at
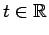
,
and take
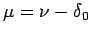
. Consider the
representation

of
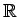
given by translation by
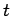
.
Then:
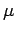
is weakly measurable;
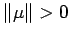
;
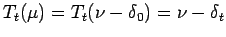
;
for every
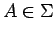
,
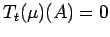
for almost all
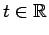
.
It now follows from Proposition
2.4 that the
representation

is not sup path attaining.
(b) Let
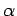
be a real number and let
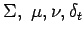
, and
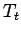
have the same meanings as in (a). Define a
representation
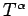
by
Arguing as in (a), it is easy to see that
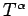
is not sup path attaining.
![]() of
of ![]() we
have
we
have
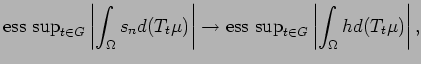
![]() is metrizable, or that
is metrizable, or that
![]() has sigma-compact support, and proceed to show that
has sigma-compact support, and proceed to show that
![]() is
weakly measurable in the sense of Definition 1.1, and that
the representation
is
weakly measurable in the sense of Definition 1.1, and that
the representation ![]() is sup path attaining.
Let
is sup path attaining.
Let
![]() is dense in
is dense in
![]() . Let
. Let
![]() be a bounded
be a bounded
![]() -measurable
function such that
-measurable
function such that
![]() for all
for all
![]() . Define
. Define ![]() as above, and let
as above, and let
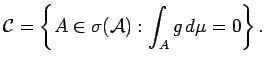
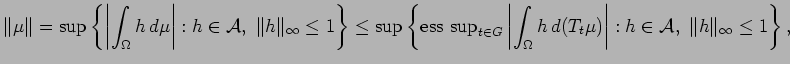
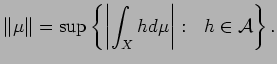
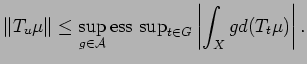
![]() .
.
![]() for which
for which
![]() depends on
depends on ![]() .
If this set were the same for all
.
If this set were the same for all
![]() , then the conclusion of the
proposition would trivially hold for
any representation by isomorphisms of
, then the conclusion of the
proposition would trivially hold for
any representation by isomorphisms of ![]() .
.