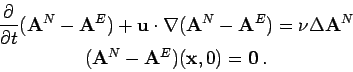Next: The decay of
Up: A counterexample to the
Previous: Properties of the operator
We will consider the following vector field in cylindrical coordinates:
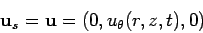 |
(4.1) |
with
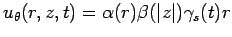 , where
, where
The vector field 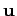 from (4.1) is divergence free and
smooth (in Cartesian coordinates
from (4.1) is divergence free and
smooth (in Cartesian coordinates 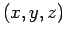 ). Evidently, there exist
). Evidently, there exist
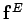 and
and
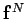 , smooth axially symmetric vector fields such that
, smooth axially symmetric vector fields such that 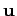 satisfies
(with constant pressure) the Euler equations and the Navier-Stokes equations,
respectively.
satisfies
(with constant pressure) the Euler equations and the Navier-Stokes equations,
respectively.
In the cylinder 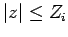 ,
, 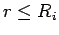 it corresponds to the rotation by the angle
it corresponds to the rotation by the angle 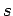 during the time interval
during the time interval ![$[0,t_0]$](img128.png) and outside of the cylinder
and outside of the cylinder 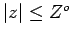 ,
, 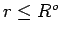 the fluid does not
move at all.
the fluid does not
move at all.
Let us start by analyzing 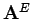 . This is actually quite easy to
compute explicitly.
Writing the input vector in cylindrical coordinates, and the output
in Cartesian coordinates, we have
. This is actually quite easy to
compute explicitly.
Writing the input vector in cylindrical coordinates, and the output
in Cartesian coordinates, we have
that is,
Inside the inner cylinder we have
outside the outer cylinder
for 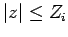 ,
,
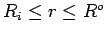
with
for
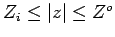 ,
, 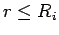
and finally for
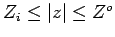 ,
,
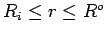 we get a combination
of the last two cases. We will use the structure of
we get a combination
of the last two cases. We will use the structure of
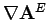 later.
later.
Let us now look at the difference between 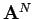 and
and 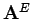 , our goal
being inequality (4.3) below. We have
, our goal
being inequality (4.3) below. We have
Taking the spatial gradient we get
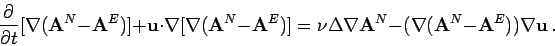 |
(4.2) |
Now, since
for some 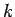 sufficiently large, we have, after testing equation (4.2)
by
sufficiently large, we have, after testing equation (4.2)
by
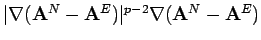
Thus, as
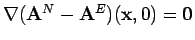 , we get
, we get
![\begin{displaymath}
\sup _{t \in [0,t_0]} \Vert\nabla (\mathbf{A}^N-\mathbf{A}^E)\Vert _p \leq \nu
C(\Vert\nabla {\mathbf{u}}\Vert _{k,2}, t_0)
\end{displaymath}](img148.png) |
(4.3) |
for all
![$p\in (1,\infty]$](img149.png) .
.



Next: The decay of
Up: A counterexample to the
Previous: Properties of the operator
Stephen Montgomery-Smith
2002-10-25
![\begin{displaymath}
\begin{array}{l}
\begin{array}{rlllrlllll}
\alpha (r) &= 0 &...
...0^{t_0} \gamma _s(\tau) d \tau = s \in
[0,2\pi]\, .
\end{array}\end{displaymath}](img121.png)
![]() ,
, ![]() it corresponds to the rotation by the angle
it corresponds to the rotation by the angle ![]() during the time interval
during the time interval ![]() and outside of the cylinder
and outside of the cylinder ![]() ,
, ![]() the fluid does not
move at all.
the fluid does not
move at all.
![]() . This is actually quite easy to
compute explicitly.
Writing the input vector in cylindrical coordinates, and the output
in Cartesian coordinates, we have
. This is actually quite easy to
compute explicitly.
Writing the input vector in cylindrical coordinates, and the output
in Cartesian coordinates, we have
![\begin{displaymath}
\begin{array}{lcr}
\mathbf{A}^E(x,y,z,t_0)& = &\Big( x \cos[...
...qrt{x^2+ y^2})
\beta (\vert z\vert) ] , z \Big)\, .
\end{array}\end{displaymath}](img132.png)
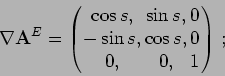
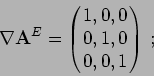
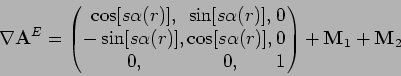
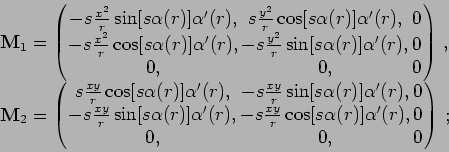
![\begin{displaymath}
\nabla \mathbf{A}^E =
\left( \begin{array}{ccc}
1, & 0, & -s...
...] \beta '(\vert z\vert)\\
0, & 0, & 1 \end{array} \right)\, ;
\end{displaymath}](img139.png)
![]() and
and ![]() , our goal
being inequality (4.3) below. We have
, our goal
being inequality (4.3) below. We have