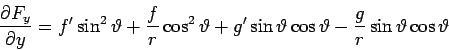Next: Construction of the Fluid
Up: A counterexample to the
Previous: Outline of the Proof
We will not prove the smoothness of solution to (1.7);
it can be done in a very standard way, using the estimates to parabolic
equations given for example in [5].
Let us only summarize the main result
here. This will show that the function 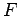 described in
Lemma 2.2 is continuous on any compact subset of
described in
Lemma 2.2 is continuous on any compact subset of
![$[0,\infty)\times[0,2\pi]$](img81.png) .
.
Lemma 3.1
Let
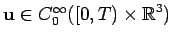 for some
for some 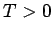 . Then,
in the class of functions
. Then,
in the class of functions
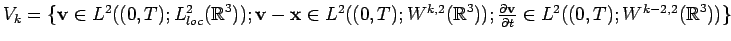 ,
, 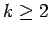 , there
exists exactly one solution to (1.7).
Moreover, this solution
is smooth, that is, in
, there
exists exactly one solution to (1.7).
Moreover, this solution
is smooth, that is, in
![$C^\infty((0,T]\times \mbox{\Bbbb R}^3) \cap
C([0,T]\times \mbox{\Bbbb R}^3)$](img86.png) ,
and
,
and
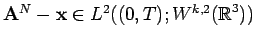 for any
for any 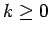 . Furthermore the solution depends smoothly upon
the choice of
. Furthermore the solution depends smoothly upon
the choice of 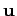 .
.
Remark 3.1 Note that if
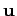
belongs to
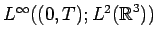
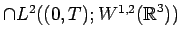
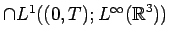
(the usual information about a weak solution to the
Navier-Stokes equations),
then only
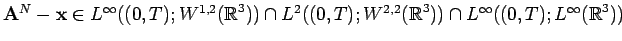
and
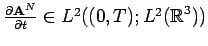
. The proof is essentially the same as the proof of Lemma
3.1 using [
5] and is left as an exercise.
Lemma 3.2
There exists an interval 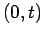 such that for
such that for 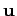 and
and 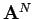 smooth as in
Lemma 3.1,
smooth as in
Lemma 3.1, 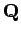 is a smooth solution to (1.8).
is a smooth solution to (1.8).
Proof: The existence of the solution can be shown using the Galerkin
method combined with standard a priori estimates. We leave the details
of the proof to the reader as an exercise.
width7pt height7pt depth0pt
Now, on the time interval from Lemma 3.2 we see that
obeys the equation (see [2])
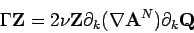 |
(3.1) |
in
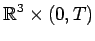 with the initial condition
with the initial condition
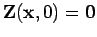 . Since,
for
. Since,
for
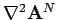 and
and
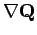 bounded, there exists the unique solution to
(3.1), we have
bounded, there exists the unique solution to
(3.1), we have
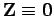 and thus
and thus
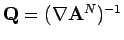 pointwise.
pointwise.
Also, we are now in a position to prove Lemma 2.1. Since
(1.7)
are uniquely solvable, it follows that
the solution is axisymmetric and hence we can apply the following result.
Proof:
Denote 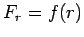 and
and
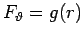 . Then we get
. Then we get
Since
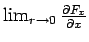 exists, necessarily
exists, necessarily
Thus
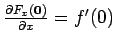 . Next
. Next
and also
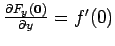 . Analogously we get that
. Analogously we get that
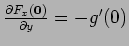 and
and
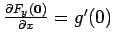 .
The lemma is proved. width7pt height7pt depth0pt
.
The lemma is proved. width7pt height7pt depth0pt



Next: Construction of the Fluid
Up: A counterexample to the
Previous: Outline of the Proof
Stephen Montgomery-Smith
2002-10-25
![]() described in
Lemma 2.2 is continuous on any compact subset of
described in
Lemma 2.2 is continuous on any compact subset of
![]() .
.
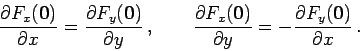
![]() and
and
![]() . Then we get
. Then we get