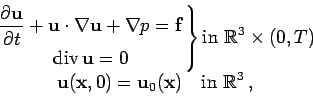Introduction

Recently there has been interest in some new variables describing the solutions to the Navier-Stokes and Euler equations. These variables go under various names, for example, the magnetization variables, impulse variables, velicity or Kuzmin-Oseledets variables.

Let us start by considering the incompressible Euler equations in the entire three-dimensional space, that is,

$$%1.1 \begin{array}{c} \left. \begin{array}{c} \displaystyle ... ...\mathbf{x}}) \quad {\rm in \ } \mbox{\Bbbb R}^3\, , \end{array}$$ (1.1)

where ${\mathbf{u}}$ and $p$ are given functions, ${\mathbf{u}}: \mbox{\Bbbb R}^3 \times(0,T) \mapsto \mbox{\Bbbb R}^3$ and $p: \mbox{\Bbbb R}^3 \times(0,T) \mapsto \mbox{\Bbbb R}$, $0<T\leq \infty$ (see Section 1 for further explanation).

The question of global existence of even only weak solutions to system (1.1) is an open question and only the existence of either measure-valued solutions (see [3]) or dissipative solutions (see [7]) is known. Nevertheless, a common approach to try to prove the global existence of smooth solutions is to use local existence results, and thus reduce the problem to proving a priori estimates. So we will assume that we have a smooth solution to the equations.

In that case, we can rewrite the Euler equations as the following system of equations (see for example [1]):

$$\begin{array}{c} \left. \begin{array}{c} \displaystyle \frac... ...\mathbf{x}}) \quad {\rm in \ } \mbox{\Bbbb R}^3\, . \end{array}$$ (1.2)

Here ${\mathbf{m}}:\mbox{\Bbbb R}^3 \times(0,T) \mapsto \mbox{\Bbbb R}^3$ is called the magnetization variable. This new formulation has several advantages to the usual one, in particular the solution can be written rather nicely in the following way. Suppose that the initial value for ${\mathbf{m}}$ may be written as

$${\mathbf{m}}({\mathbf{x}},0) = \sum_{i=1}^R \beta_i({\mathbf{x}},0) \nabla \alpha_i({\mathbf{x}},0) ,$$ (1.3)

and suppose that $\alpha$ and $\beta$ satisfy the transport equations, that is

$$\begin{array}{c} \displaystyle \frac {\partial \alpha_i}{\pa... ...u}}\cdot \nabla \beta_i = \sum_{j=1}^R Q_{j,i} f_j \end{array}$$

where ${\mathbf{Q}}= (Q_{i,j})$ is the matrix inverse of the matrix whose entries are $\frac {\partial \alpha_i}{\partial x_j}$. (There is some difficulty to suppose that this inverse exists unless $R=3$ -- see below. But generally this will not be a problem if ${\mathbf{f}}= 0$.) Then

$${\mathbf{m}}({\mathbf{x}},t) = \sum_{i=1}^R \beta_i({\mathbf{x}},t) \nabla \alpha_i({\mathbf{x}},t)$$

is the solution to system (1.2). That is to say, at least in the case that ${\mathbf{f}}= 0$, the magnetization variable may be thought of as a ``1-form'' acting naturally under a change of basis induced by the flow of the fluid.

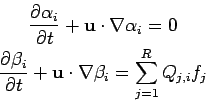
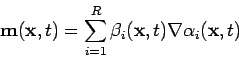
The advantage of the magnetization variable is that it is local in that its support never gets larger, it is simply pushed around by the flow. It is only at the end, after one has calculated the final value of ${\mathbf{m}}$, that one needs to take the Leray projection to compute the velocity field ${\mathbf{u}}$.

Indeed one very explicit way to write ${\mathbf{m}}$ according to equation (1.3) is to set $\alpha_i({\mathbf{x}},0)$ equal to the $i$th unit vector, and $\beta_i({\mathbf{x}},0) = u_i({\mathbf{x}},0)$, for $1 \le i \le R = 3$. In that case let us denote $A^E_i({\mathbf{x}},t) = \alpha_i({\mathbf{x}},t)$ and $v_i({\mathbf{x}},t) = \beta_i({\mathbf{x}},t)$. In that case we see that $\mathbf{A}^E({\mathbf{x}},t)$ is actually the back to coordinates map, that is, it denotes the initial position of the particle of fluid that is at ${\mathbf{x}}$ at time $t$ (see for example [1]). Furthermore in the case that ${\mathbf{f}}= 0$, we see that ${\mathbf{v}}({\mathbf{x}},t) = {\mathbf{u}}_0(\mathbf{A}^E({\mathbf{x}}))$. Furthermore, it is well known if ${\mathbf{u}}$ is smooth, that $\mathbf{A}^E(\cdot,t)$ is smoothly invertible, and that the determinant of the Jacobian of $\mathbf{A}^E$ is identically equal to $1$ (because $\div {\mathbf{u}}= 0$). Hence the matrix ${\mathbf{Q}}$ exists. For definiteness, we write the explicit equation for ${\mathbf{m}}$:

$$%1.2 m_i({\mathbf{x}},t) = \frac {\partial \mathbf{A}^E({\ma... ...x}}, t)}{\partial x_i} \cdot {\mathbf{v}}^E({\mathbf{x}}, t) .$$ (1.4)

The desire, then, is to try to extend this notion to the Navier-Stokes equations

$$%{1.3} \begin{array}{c} \left. \begin{array}{c} \displaysty... ...\mathbf{x}}) \quad {\rm in \ } \mbox{\Bbbb R}^3\, . \end{array}$$ (1.5)

(Only local-in-time existence of smooth solutions to the Navier-Stokes equations is known -- see for example [4]; globally in time, only existence of weak solutions is known, see [6].)

Again, these can be rewritten into the magnetic variables formulation as follows:

$$%{1.3a} \begin{array}{c} \left. \begin{array}{c} \displayst... ...\mathbf{x}}) \quad {\rm in \ } \mbox{\Bbbb R}^3\, . \end{array}$$ (1.6)

The problem is to find the analogue of equation (1.4). The difficulty comes from the term $\nu \Delta {\mathbf{m}}$. There are two ways known to the authors -- one is to use probabilistic techniques. Since this technique seems to be not as widely known as it should be, we will include a short (non-rigorous) description of this method at the end of the paper. We will also include a short plausibility argument for the global regularity for the Navier-Stokes equations.

Another approach was developed by Peter Constantin (see [2]). He used new quantities $\mathbf{A}^N$ and ${\mathbf{v}}^N$ obeying the following equations. Let us represent ${\mathbf{u}}$ in a form similar to (1.2)

$$u_i({\mathbf{x}},t) = \frac {\partial \mathbf{A}^N({\mathbf{... ...{x}},t) - \frac {\partial n({\mathbf{x}},t)}{\partial x_i}\, ,$$

where

$$\begin{array}{c} \Gamma (\mathbf{A}^N) = {\mathbf {0}}\qquad... ... = {\mathbf{x}}\qquad {\rm in \ } \mbox{\Bbbb R}^3 \end{array}$$ (1.7)

$$\Gamma = \frac {\partial }{\partial t} + {\mathbf{u}}\cdot \nabla - \nu \Delta\, ,$$

and ${\mathbf{v}}^N$ obeys a rather complicated equation

$$\Gamma (v^N_i) = 2 \nu C_{m,k;i} \frac {\partial v_m}{\partial x_k} + Q_{j,i} f_j\, ,$$

where ${\mathbf{Q}}$ is the inverse matrix to $\nabla \mathbf{A}^N$ and $\Gamma_{i,j}^m = - Q_{k,j} C_{m,k;i}$ denotes the Christoffel coefficients. In order for the equation for ${\mathbf{v}}$ to make sense, it is necessary for the map $\mathbf{A}^N$ to have a smooth inverse. An approach to proving such a result is to consider the system of PDE's

$$% {0.1} \begin{array}{c} \Gamma ({\mathbf{Q}}) = (\nabla {\m... ...{\mathbf{I}}\qquad {\rm in \ } \mbox{\Bbbb R}^3\, , \end{array}$$ (1.8)

If the above equations have smooth solutions, then it can easily be shown that ${\mathbf{Q}}$ is the inverse to $\nabla \mathbf{A}^N$. However, the problem is that while it is easy and standard to show that equation (1.8) has local smooth solutions, it is not clear that it has global solutions in any sense at all.

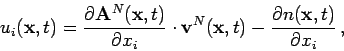
The purpose of this note is to show that indeed global smooth solutions do not exist. As Peter Constantin pointed out to us, this does not invalidate his method, but it does mean that to make his method work for a large time period that one has to break that interval into shorter pieces, and apply the method to each small interval.

The main result is summarized in the following theorem.

Theorem 1.1   There exists ${\mathbf{u}}\in C^\infty_0(\mbox{\Bbbb R}^3 \times [0,\infty))$, divergence free such that if $\mathbf{A}^N$ is a smooth solution to (1.7) then there exists $t>0$ such that

(a)

$\mathbf{A}^N({\mathbf {0}}, t)$ does not have a smooth inverse

(b)

$\limsup_{\tau \to t^-} \Vert{\mathbf{Q}}\Vert _\infty(\tau) = \infty$,

where ${\mathbf{Q}}$ is a solution to (1.8) corresponding to ${\mathbf{u}}$ and $\mathbf{A}^N$.