Integrals, Sums and Limits

Here is the integral symbol

integral

$$\int$$

Here is the integral sign used: note the optional use of `of'. Also `dx' is a single symbol. It can be expressed as two separate symbols, but the use of the single symbol slightly improves the typesetting.

integral x^3 dx,
integral of x^3 dx,
integral of x^3 d x

$$\int {x} ^ {3} \,d x , \ \int {x} ^ {3} \,d x , \ \int {x} ^ {3} d x$$

Definite integrals are a little trickier, because Natural Math has to figure out what should be in the limits. It will make an intelligent guess, but sometimes it needs help. This can be provided, either with brackets, or with `of'.

integral from 1 to a + b x^3 dx,
integral from 1 to a b x^3 dx,
integral from 1 to (a b) x^3 dx,
integral from 1 to a b of x^3 dx

$$\int _ {1} ^ {a + b} {x} ^ {3} \,d x , \ \int _ {1} ^ {a} b ... ...^ {a b} {x} ^ {3} \,d x , \ \int _ {1} ^ {a b} {x} ^ {3} \,d x$$

Sums are exactly the same. The following example shows that you don't need to use both of the `from' and `to' quantifiers.

sum from n <= 20 of a_n

$$\sum _ {n \le 20} {a} _ {n}$$

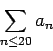
Limits are similar: we have the `as' quanitifier:

rho = lim as n to infinity | a_(n+1) over a_n | ,
rho = lim as n to infinity of | a_(n+1) over a_n | ,

$$\rho = \lim _ {n \to \infty} \left\vert \frac {{a} _ {n + 1}... ... \left\vert \frac {{a} _ {n + 1}} {{a} _ {n}} \right\vert , \$$

`From' and `to' may also be used with brackets (both round and square), although instead of `of' you can use `end'.

[ x^3 ] from 0 to 6 / a end ,
[ x^3 ] from 0 to 6 / a ,
[ x^3 ] from 0 to (6 / a)

$$\left[ {x} ^ {3} \right] _ {0} ^ {6 / a} , \ \left[ {x} ^ {3... ...] _ {0} ^ {6} / a , \ \left[ {x} ^ {3} \right] _ {0} ^ {6 / a}$$

More examples:

integral u dv over dx dx = u v - integral v du over dx dx

$$\int u \frac {\,d v} {\,d x} \,d x = u v - \int v \frac {\,d u} {\,d x} \,d x$$

integral from 0 to 10 of theta^3 dtheta
=
[x^4 over 4] from 0 to 10
=
10^4 over 4 - 0^4 over 4
=
1000 over 4

$$\int _ {0} ^ {10} {\theta} ^ {3} \,d \theta = \left[ \frac {... ...ac {{10} ^ {4}} {4} - \frac {{0} ^ {4}} {4} = \frac {1000} {4}$$

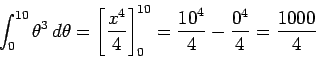
integral from -1 to 1 1 over x^(2/3) dx
=
limit as a to 0^- of
integral from -1 to a 1 over x^(2/3) dx
+ 
limit as b to 0^+ of
integral from b to 1 1 over x^(2/3) dx

$$\int _ { - 1} ^ {1} \frac {1} {{x} ^ {2 / 3}} \,d x = \lim _... ...to {0} ^ {+}} \int _ {b} ^ {1} \frac {1} {{x} ^ {2 / 3}} \,d x$$

= 
limit as a to 0^- of
[3 x^(1/3) ] from -1 to a
+ 
limit as b to 0^+ of
[3 x^(1/3) ] from b to 1

$$= \lim _ {a \to {0} ^ {-}} \left[ 3 {x} ^ {1 / 3} \right] _... ..._ {b \to {0} ^ {+}} \left[ 3 {x} ^ {1 / 3} \right] _ {b} ^ {1}$$

Note that in the last example, the use of the `of's is rather crucial. See what happens if we don't use them:

= 
limit as a to 0^-
[3 x^(1/3) ] from -1 to a
+ 
limit as b to 0^+
[3 x^(1/3) ] from b to 1

$$= \lim _ {a \to {0} ^ { - \left[ 3 {x} ^ {1 / 3} \right] _ ... ...{b \to {0} ^ { + \left[ 3 {x} ^ {1 / 3} \right] _ {b} ^ {1}}}}$$