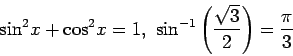Functions

Natural Math supports a range of functions

sqrt a, abs a, |a|, a squared, a !, a factorial

$$\sqrt{a} , \ \left\vert a \right\vert , \ \left\vert a \right\vert , \ {a} ^ 2 , \ a ! , \ a !$$

and the trig and hyperbolic functions:

sin, cos, tan, sec, csc, cot, 
arcsin, arccos, arctan, 
sinh, cosh, tanh, coth

$$\sin , \ \cos , \ \tan , \ \sec , \ \csc , \ \cot , \ \arcsin , \ \arccos , \ \arctan , \ \sinh , \ \cosh , \ \tanh , \ \coth$$

and functions that you can create yourself, either by using quotes, or by using the ``textsymb'' command:

"sech"(x) = textsym sech(x) = 2 over (e^x + e^-x)

$$\hbox{sech} \left( x \right) = \hbox{sech} \left( x \right) = \frac {2} {{e} ^ {x} + {e} ^ { - x}}$$

Some of these functions interact with brackets in interesting ways:

sqrt(a+b) , sqrt((a+b)) , abs(a+b) , abs((a+b))

$$\sqrt{a + b} , \ \sqrt{\left( a + b \right)} , \ \left\vert a + b \right\vert , \ \left\vert \left( a + b \right) \right\vert$$

The absolute value construction is even more interesting, and there is a potential for ambiguity: does $\vert a\vert b\vert c\vert$ represent $\hbox{abs}(a\,\hbox{abs}(b)\,c)$, or $\hbox{abs}(a)\,b\,\hbox{abs}(c)$? Natural Math will use the second interpretation, but this can be changed using brackets:

|x over y| 5 |x over y|,
|(x over y| 5 |x over y)|

$$\left\vert \frac {x} {y} \right\vert 5 \left\vert \frac {x} ... ...rac {x} {y} \left\vert 5 \right\vert \frac {x} {y} \right\vert$$

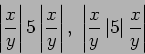
Finally, the trig functions can be raised to powers:

sin^2 x + cos^2 x = 1,
sin^-1 (sqrt3 over 2) = pi over 3

$${\sin} ^ {2} x + {\cos} ^ {2} x = 1 , \ {\sin} ^ { - 1} \left( \frac {\sqrt{3}} {2} \right) = \frac {\pi} {3}$$