Keywords: Navier-Stokes equation, semigroup, fixed point method, Triebel-Lizorkin space, Besov space.
A.M.S. Classification (2000): Primary 35Q30, 46E35; Secondary 34G20, 37L05, 47D06, 47H10.
Stephen Montgomery-Smith1
Department of Mathematics
University of Missouri
Columbia, MO 65211
stephen@math.missouri.edu
http://faculty.missouri.edu/~stephen
In this paper, we consider a simplified model for the Navier-Stokes equation -- what we call the cheap Navier-Stokes equation. For this equation, we show that for sufficiently large initial data, that we get blow up in finite time. The purpose of this is not to indicate the possibility that the Navier-Stokes equation might blow up in finite time -- indeed the author strongly believes the opposite. Rather, the purpose of this paper is to show limitations in some of the methods used in studying the Navier-Stokes equation.
Let us consider the following version of the Navier-Stokes equation:
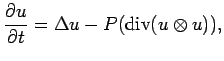
However, if one studies all these papers, one sees that they do not use all of the properties of the Navier-Stokes equation. Indeed, the methods seem to apply equally well to the the following equation, the cheap Navier-Stokes equation:
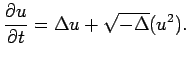 |
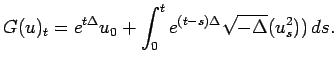 |
The semigroup
method by itself never seems to be able to obtain global results, that is,
results valid for both ![]() and the size of
and the size of ![]() arbitrarily large.
To obtain global results, one has to appeal to other
kinds of estimates for the Navier-Stokes equation, for example, energy
estimates (see, for example, [KF] or [Ca2]).
arbitrarily large.
To obtain global results, one has to appeal to other
kinds of estimates for the Navier-Stokes equation, for example, energy
estimates (see, for example, [KF] or [Ca2]).
The purpose of this paper is to show that the semigroup method really is limited in this way. For if we could obtain global results for the Navier-Stokes equation using only the semigroup method, then the same methods would also apply to the cheap Navier-Stokes equation. This would then contradict the main result of this paper and its corollary.
Thus, if one is going to obtain global results for the Navier-Stokes
equation, one has to consider properties of the bilinear form
![]() that are not shared by the bilinear form
that are not shared by the bilinear form
![]() . Perhaps there is some mysterious cancellation
property in the first bilinear form that causes global regularity for
the Navier-Stokes equation. In any case, the semigroup technique in
of itself, at least in the manner in which it has been applied to date,
is not going to solve the problem.
. Perhaps there is some mysterious cancellation
property in the first bilinear form that causes global regularity for
the Navier-Stokes equation. In any case, the semigroup technique in
of itself, at least in the manner in which it has been applied to date,
is not going to solve the problem.
Let ![]() denote the first unit vector in
denote the first unit vector in
![]() , and for
, and for
![]() ,
,
![]() , let
, let ![]() denote
denote
![]() .
Let
.
Let ![]() denote the Fourier transform of
denote the Fourier transform of ![]() with
respect to
with
respect to
![]() .
.
We also present another result about the
cheap Navier-Stokes
equation. For the Navier-Stokes equation (and hence also for the
cheap Navier-Stokes equation), it turns out that the natural spaces
in which to consider solutions are of the form
![]() , where
, where ![]() is scale invariant, that is,
is scale invariant, that is,
![]() for all
for all
![]() .
Authors have considered which is the
largest scale invariant space for which one gets existence
results. For example, recently Koch and Tataru [KT] showed such
results when
.
Authors have considered which is the
largest scale invariant space for which one gets existence
results. For example, recently Koch and Tataru [KT] showed such
results when ![]() is the space of derivatives of functions with
bounded mean oscillation.
is the space of derivatives of functions with
bounded mean oscillation.
In fact, it can be shown (arguing similarly as in Frazier, Jawerth and Weiss
in [FJW] for the minimality of ![]() )
that all scale invariant spaces of distributions,
that also contain all Schwartz functions, are
contained in the Besov space
)
that all scale invariant spaces of distributions,
that also contain all Schwartz functions, are
contained in the Besov space
![]() .
Cannone [Ca1] was able to obtain results for the Navier-Stokes
equation in the space
.
Cannone [Ca1] was able to obtain results for the Navier-Stokes
equation in the space
![]() ,
,
![]() , but left open the case
, but left open the case ![]() corresponding
to the space
corresponding
to the space
![]() .
.
We will respond to this last case negatively for
the cheap Navier-Stokes equation. Although this does not answer
the question for the Navier-Stokes equation, the author believes that
it is very possible that there is a similar non-existence result
for the Navier-Stokes equation. But this would say more about the
nature of the space
![]() than about the
Navier-Stokes equation itself.
than about the
Navier-Stokes equation itself.
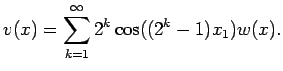
The crucial observation for all these results is that the cheap Navier-Stokes equation is that
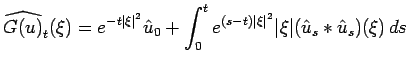 |
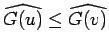 .
.
Proof of Theorem 1:
Using the usual embedding theorems, it may be seen that all of the
Triebel-Lizorkin and Besov spaces
embed into
![]() for some
for some
![]() .
Let us recall the definition of the Besov space
.
Let us recall the definition of the Besov space
![]() .
Let
.
Let ![]() be some
tempered Schwartz function
whose Fourier transform is non-negative,
whose support is ``mostly'' contained
in a band about
be some
tempered Schwartz function
whose Fourier transform is non-negative,
whose support is ``mostly'' contained
in a band about
![]() , and such that
, and such that
![]() is uniformly bounded above and below.
Here
is uniformly bounded above and below.
Here
![]() .
Then
.
Then
![]() is the space of
distributions on
is the space of
distributions on
![]() for
which the norm
for
which the norm
![]() is finite.
is finite.
Write ![]() for the function
for the function
![]() ,
and set
,
and set
![]() . Since
. Since ![]() and
and ![]() are real valued,
we see that
are real valued,
we see that ![]() must be an even function.
Hence we quickly see that
must be an even function.
Hence we quickly see that
![]() has
has ![]() norm equal to
norm equal to ![]() , and is supported in
, and is supported in
![]() .
.
We will show by induction
that
![]() for
for ![]() ,
where
,
where
![]() ,
,
![]() , and
, and
![]() .
The case
.
The case ![]() follows since
follows since
![]() .
Suppose that our desired inequality holds for
.
Suppose that our desired inequality holds for ![]() . Then
. Then
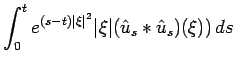 |
|||
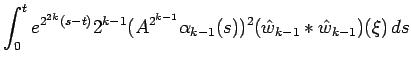 |
|||
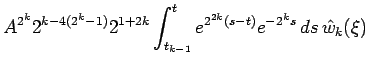 |
|||
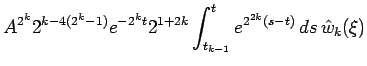 |
|||
Let
![]() .
Since
.
Since
![]() ,
,
Proof of Corollary 2:
Suppose for a contradiction that there is a solution
![]() . By the methods of [K],
we know that there is a
number
. By the methods of [K],
we know that there is a
number
![]() , depending only upon
, depending only upon
![]() , such that
for every
, such that
for every
![]() that there is a mild solution
that there is a mild solution
![]() to the cheap Navier-Stokes equation,
with
to the cheap Navier-Stokes equation,
with ![]() , that is obtained by starting with
, that is obtained by starting with
![]() ,
and iterating a function
,
and iterating a function ![]() similar to that defined above.
By the uniqueness result of Furioli, Lemarié-Rieusset
and Terraneo [FLT],
we have that
similar to that defined above.
By the uniqueness result of Furioli, Lemarié-Rieusset
and Terraneo [FLT],
we have that ![]() for
for
![]() .
From this it is clear that if
.
From this it is clear that if
![]() , then
, then
![]() for
for
![]() . Applying this argument
several times, we see that
. Applying this argument
several times, we see that
![]() for
for
![]() .
Then by Theorem 1,
.
Then by Theorem 1, ![]() is not in any
Triebel-Lizorkin space, and hence in particular is not in
is not in any
Triebel-Lizorkin space, and hence in particular is not in
![]() .
.
Proof of Theorem 3:
Suppose we have a non-negative solution
![]() to
the cheap Navier-Stokes equation with
to
the cheap Navier-Stokes equation with ![]() . It is clear that
. It is clear that
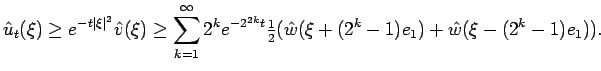
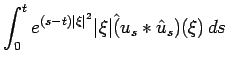 |
|||
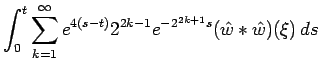 |
|||
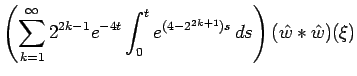 |
|||
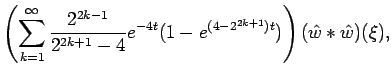 |
The author would like to thank Marco Cannone for many useful discussions and helpful remarks.