Example

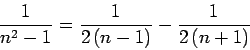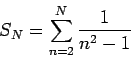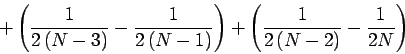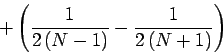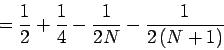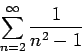
# Start the question

text Chapter 8.6 Question 25

text Evaluate the following sum

sum from n = 2 to infinity of 1 over (n^2 - 1)

text Answer: use partial fractions

n^2 - 1 = (n-1)(n+1)

1 over (n^2 - 1) = A over (n-1) + B over (n + 1)

= (A(n+1) + B (n-1)) over ((n-1)(n+1))

1 = A n + A + B n - B

text Equate coefficients

0 = A - B

1 = A + B

text add equations

1 = 2A

A = 1 over 2

B = - 1 over 2

1 over (n squared - 1) = 1 over (2(n-1)) - 1 over (2(n+1))

S _ N = sum from n = 2 to N of 1 over (n^2 - 1)

=
(1 over 2 - 1 over 6) + (1 over 4 - 1 over 8) + (1 over 6 - 1 over 10)
+ (1 over 8 - 1 over 12)
+ ... +

+ (1 over (2(N-3)) - 1 over (2(N-1)) )
+ (1 over (2(N-2)) - 1 over (2N) )

+ (1 over (2(N-1)) - 1 over (2(N+1)) )

=
1 over 2 + 1 over 4 - 1 over (2N) - 1 over (2(N+1))

limit as N to infinity of S_N = 3 over 4

Chapter 8.6 Question 25

Evaluate the following sum

$$\sum _ {n = 2} ^ {\infty} \frac {1} {{n} ^ {2} - 1}$$

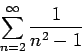
Answer: use partial fractions

$${n} ^ {2} - 1 = \left( n - 1 \right) \left( n + 1 \right)$$

$$\frac {1} {{n} ^ {2} - 1} = \frac {A} {n - 1} + \frac {B} {n + 1}$$

$$= \frac {A \left( n + 1 \right) + B \left( n - 1 \right)} {\left( n - 1 \right) \left( n + 1 \right)}$$

$$1 = A n + A + B n - B$$

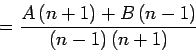
Equate coefficients

$$0 = A - B$$

$$1 = A + B$$

add equations

$$1 = 2 A$$

$$A = \frac {1} {2}$$

$$B = - \frac {1} {2}$$

$$\frac {1} {{n} ^ 2 - 1} = \frac {1} {2 \left( n - 1 \right)} - \frac {1} {2 \left( n + 1 \right)}$$

$${S} _ {N} = \sum _ {n = 2} ^ {N} \frac {1} {{n} ^ {2} - 1}$$

$$= \left( \frac {1} {2} - \frac {1} {6} \right) + \left( \fr... ...ht) + \left( \frac {1} {8} - \frac {1} {12} \right) + \dots +$$

$$+ \left( \frac {1} {2 \left( N - 3 \right)} - \frac {1} {2 ... ...( \frac {1} {2 \left( N - 2 \right)} - \frac {1} {2 N} \right)$$

$$+ \left( \frac {1} {2 \left( N - 1 \right)} - \frac {1} {2 \left( N + 1 \right)} \right)$$

$$= \frac {1} {2} + \frac {1} {4} - \frac {1} {2 N} - \frac {1} {2 \left( N + 1 \right)}$$

$$\lim _ {N \to \infty} {S} _ {N} = \frac {3} {4}$$